Cachis... Se me escapó una entrada. Si alguien la ha visto, que la olvide hasta el próximo domingo por la tarde. Aún no estaba acabada :(

Lenguajes esotéricos

Este artículo es una reedición, con algunos extras nuevos, del que publiqué en la columna Informática recreativa en la ahora extinta web de Lola Cárdenas El rincón del programador. También fue publicada con mi permiso en programacion.com. Pido disculpas si algunos enlaces no funcionan. También pido disculpas por el uso repetido de la palabra decrementar a lo largo del texto, no reconocida en el DRAE.

---

Ser aficionado a la informática y no saber programar es algo que no casa bien. Un auténtico aficionado sabrá al menos hacer pinitos en algún lenguaje de programación, sea Java, Basic, Pascal, C o cualquier otro. Entre los lenguajes de programación también hay modas; un cierto lenguaje «se lleva» más que otros en ciertos momentos, lo cual es lógico habida cuenta de que la informática evoluciona y con ella las necesidades.

No muchos conocen, sin embargo, la inmensa variedad de lenguajes de programación que hay disponibles. Los nombres que ahora mismo me vienen a la cabeza sin consultar ninguna fuente de información son COBOL, ALGOL, APL, BASIC, RPG, Forth, Fortran, Lisp, PL/I, Logo, C, Pascal, Perl, Python, TCL, Ada, Java, ensamblador... y he omitido deliberadamente nombrar variantes como Visual Basic, RPG III, Scheme (un derivado de Lisp), C++ o Delphi (un Pascal ampliado).

Cuando llegamos al ensamblador, el tema de las variantes se convierte en locura. Cada modelo de microprocesador tiene su propio ensamblador, y existen miles y miles de modelos: Z80, PIC-16, 8051, 8086, 6809, 68000, 6502... A veces, como en el caso del 80x86 de Intel, hay varios, incluso multitud de dialectos: el dialecto oficial de Intel, el dialecto oficial del proyecto GNU (formato AT&T), el dialecto del ensamblador gratuito NASM...

Para liar aún más la madeja existen personas que inventan su propio lenguaje ensamblador, el de un procesador que no existe. El ejemplo más notable quizá sea el de Donald Ervin Knuth, matemático y escritor de una serie de tratados sobre computación famosos en todo el mundo. Existen simuladores de los dos lenguajes ensambladores que ha inventado, que corresponden a los procesadores imaginarios llamados MIX y MMIX.

Ahí no queda todo. Hay gente que no ve razón en que el lenguaje a inventar sea un lenguaje ensamblador; simplemente inventan un lenguaje nuevo. Las razones son muy variadas; está claro por ejemplo que Sun Microsystems tenía razones poderosas para inventar el Java. Pero no todo el mundo necesita razones poderosas; aquí vamos a tratar precisamente sobre los lenguajes de programación que han sido inventados por puro entretenimiento. ¿Hay gente capaz de eso? Sí, y no pocos. Incluso existen intérpretes de la mayoría de esos lenguajes, y en algunos casos hasta compiladores.

Uno de los primeros lenguajes esotéricos (al menos que yo tenga referencia, pues fue creado en 1972), y quizá de los más extendidos, es el INTERCAL. Su diseño se fundamenta en la pretensión de crear un lenguaje totalmente distinto a cualquier otro en todo, aunque sin olvidar desde luego el sentido del humor. En él, tenemos que pedir por favor la ejecución de ciertas sentencias; en lugar del conocido «go to» (ir a) para saltar a otra instrucción, tenemos que escribir «come from» (venir desde) en el lugar de destino, aunque esto es una extensión posterior a la primera especificación. Podemos pedir que se abstenga de ejecutar ciertas sentencias, por ejemplo: PLEASE ABSTAIN FROM CALCULATING evita que se ejecute la orden CALCULATE. Cuando llegamos al capítulo sobre la precedencia de operadores se nos explica que no la hay, porque precisamente el objetivo en el diseño del lenguaje era que no hubiera ningún precedente. Como resultado de esta regla, cuando necesitamos concatenar dos operaciones juntas hay que agrupar los operandos por pares mediante un equivalente a los paréntesis. El nombre completo del lenguaje, según los autores, es «Lenguaje Compilado Carente de Acrónimo Pronunciable», cuya abreviatura es, «por razones obvias», INTERCAL. Podemos ver el aspecto que tiene un programa escrito en INTERCAL en la figura 1. La función de este programa, extraído del manual de INTERCAL, es leer dos enteros de 32 bits, tratándolos como enteros con signo en formato de complemento a dos, y escribir su valor absoluto.

        DO (5) NEXT
    (5) DO FORGET #1
        PLEASE WRITE IN :1
        DO .1 <- 'V":1~'#32768$#0'"$#1'~#3
        DO (1) NEXT
        DO :1 <- "'V":1~'#65535$#0'"$#65535'
                ~'#0$#65535'"$"'V":1~'#0$#65535'"
                $#65535'~'#0$#65535'"
        DO :2 <- #1
        PLEASE DO (4) NEXT
    (4) DO FORGET #1
        DO .1 <- "'V":1~'#65535$#0'"$":2~'#65535
                $#0'"'~'#0$#65535'"$"'V":1~'#0
                $#65535'"$":2~'#65535$#0'"'~'#0$#65535'"
        DO (1) NEXT
        DO :2 <- ":2~'#0$#65535'"
                $"'":2~'#65535$#0'"$#0'~'#32767$#1'"
        DO (4) NEXT
    (2) DO RESUME .1
    (1) PLEASE DO (2) NEXT
        PLEASE FORGET #1
        DO READ OUT :1
        PLEASE DO .1 <- 'V"':1~:1'~#1"$#1'~#3
        DO (3) NEXT
        PLEASE DO (5) NEXT
    (3) DO (2) NEXT
        PLEASE GIVE UP

Figura 1: Programa en lenguaje INTERCAL

Los programas en INTERCAL, desde luego, no son fáciles de escribir. De todas formas no es el lenguaje esotérico en el que más cuesta escribir un programa. Por ejemplo, en lenguaje Piet es imposible escribir un programa: hay que dibujarlo. Vemos en la figura 2 un ejemplo de un programa en lenguaje Piet.

Figura 2: Programa en lenguaje Piet.

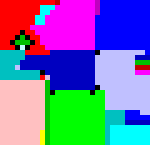
El programa de la figura 2 se limita a escribir la conocida frase «Hello, world!» («¡Hola, mundo!»). Hay que reconocer, sin embargo, que hemos hecho abuso del significado de la palabra escribir en este contexto. Diseñar el programa es algo que en Piet no es una tarea demasiado difícil.

Quien busque algo en lo que sea verdaderamente difícil programar, puede intentar usar Malbolge. El nombre procede del Malebolge (el octavo círculo del infierno de Dante), aunque seguramente el nombre fue recortado a causa de una limitación del sistema operativo para el que fue originariamente escrito (MS-DOS), que limita la longitud de los nombres a ocho caracteres. Esta alusión al infierno puede dar una somera idea de la complicación del lenguaje, aunque obtendremos una idea más aproximada conociendo la dificultad que supuso para Andrew Cooke escribir un programa en Malbolge que simplemente escribiera «Hello, world» (digamos que lo hizo por métodos de tipo «ensayo y error», y ni siquiera consiguió uniformidad en las mayúsculas y minúsculas ni signos de puntuación: el programa escribía «HEllO WORld»). En la figura 3 vemos el programa que consiguió la hazaña.

(=<`$9]7<5YXz7wT.3,+O/o'K%$H"'~D|#z@b=`{^Lx8%$Xmrkpohm-kNi;g
sedcba`_^]\[ZYXWVUTSRQPONMLKJIHGFEDCBA@?>=<;:9876543s+O<oLm

Figura 3: Programa en lenguaje Malbolge.

No hay que desesperarse por no entender nada. Esa es justo la intención que el inventor del lenguaje tenía. De hecho, el cripticismo buscado por el autor le resta cierto interés al lenguaje: está deliberadamente encriptado, razón por la cual Cooke propone un «Malbolge normalizado», que es lo que queda después de la fase de desencriptación. No hay que dejarse llevar por la idea, sin embargo, de que esto le reste dificultad al lenguaje. Se puede (si es que se puede) escribir un programa en Malbolge normalizado y después aplicar la fase final de encriptación para obtener un programa válido en Malbolge. La figura 4 muestra el aspecto del programa «Hello world» en Malbolge normalizado.

jpp<jp<pop<<jo*<popp<o*p<pp<pop<pop<jijoj/o<vvjpopoopo<ojo/o
vooooooooooooooooooooooooooooooooooooooooooooooooooo*p<v*<*

Figura 4: Programa en lenguaje Malbolge normalizado.

Aunque resulta algo más legible que antes, sigue siendo complicado de descifrar sin una descripción de qué significa cada símbolo (y aun con ella). En el fichero de la distribución de Malbolge existe una descripción completa del lenguaje.

Pero de entre todos los lenguajes esotéricos hay uno que llama la atención por su exquisita simplicidad y potencia. Se llama Brainfuck, que en inglés suena tan mal como en español su traducción de Jodecerebros, con perdón. Debido a lo ofensivo del nombre, no es tan fácil buscar referencias en WWW usando buscadores ya que hay muchas variaciones del nombre para ocultar su carácter ofensivo: Brainf*ck, Brainf***, Brainfsck, BF... La intención de su creador, Urban Müller, era la de crear un lenguaje para el cual se pudiera escribir el compilador más corto del mundo.

A pesar del nombre, escribir un programa en Brainfuck no es tan difícil como cabe pensar. Está demostrado que es un lenguaje Turing-completo, lo que expresado de forma simple significa que se puede codificar cualquier algoritmo con él. Existen únicamente ocho instrucciones, cada una de las cuales está asociada a un símbolo. Hay un resumen en la tabla 1. Existe un puntero de programa, que representa la posición en la que se está ejecutando actualmente el código, como en cualquier otro lenguaje imperativo (con algunas salvedades), y un puntero de datos, que es una característica propia de Brainfuck y que sirve precisamente para manipular los datos. El puntero de datos apunta a la posición cero de una zona de memoria, inicialimente rellena de ceros. No se considera correcto un programa si intenta aplicar un decremento al puntero de datos cuando éste está en la posición cero. Usualmente se considera que el contenido de cada posición de memoria es un byte sin signo (un número de 0 a 255). Al incrementar uno de estos bytes cuando su valor era 255, generalmente pasa a valer 0. Al aplicarle un decremento cuando su valor era 0, generalmente pasa a valer 255. Decimos «generalmente» porque según la implementación puede haber versiones del lenguaje que adopten otros convenios.

Instrucción	Descripción	Equivalente C
-	Restar 1 al contenido de la celda de memoria actualmente apuntada por el puntero de datos.	--*p;
+	Sumar 1 al contenido de la celda de memoria actualmente apuntada por el puntero de datos.	++*p;
<	Decrementar el puntero de datos en una unidad. Es un error ejecutar esta instrucción cuando el puntero de datos tiene el valor 0.	--p;
>	Incrementar el puntero de datos en una unidad.	++p;
[	Si el contenido de la celda de memoria a la que apunta el puntero de datos es cero, buscar el correspondiente «]» y colocar el puntero de instrucción inmediatamente después. Es posible anidarlos. No se considera un programa válido aquél en el que no hay un balance correcto entre los «[» y los «]».	while(*p){
]	Colocar el puntero de programa en el «[» anterior correspondiente.	}
,	Introducir un carácter desde entrada estándar y colocarlo en la celda apuntada por el valor actual del puntero de datos.	*p=getchar();
.	Escribir el carácter ASCII correspondiente al valor de la celda actual en la salida estándar.	putchar(*p);

Tabla 1: Instrucciones del lenguaje Brainfuck.

Aquellos que sepan C pueden valerse de las equivalencias aproximadas que se dan en la tabla para entender un poco mejor las acciones que cada instrucción realiza. Con tal sencillez estructural, mal puede sorprendernos la facilidad con la que se puede escribir un intérprete, y hasta un compilador de Brainfuck. Pero antes de entrar en detalles respecto al intérprete, analizaremos un poco el lenguaje y veremos algunas construcciones comunes.

Por ejemplo, la secuencia de instrucciones [-] se usa a menudo en los programas Brainfuck, y sirve para poner a cero la celda de memoria actual: equivale en C a la instrucción «while(*p){--*p;}», es decir, mientras la celda de memoria actual sea distinta de cero, decrementarla, lo cual obviamente tiene como efecto ponerla a cero.

Si queremos mover el valor actual una posición a la derecha (aquí entendemos que «izquierda» implica disminuir el puntero de datos y «derecha» aumentarlo), utilizaremos el siguiente programa: [>+<-]. Esto va incrementando el byte de la derecha de la posición inicial y decrementando el actual, hasta que éste es cero. Como resultado, al byte situado a la derecha de la posición inicial se le suma lo que hubiera en dicha posición, que acaba siendo cero. Suponiendo que a la derecha hubiera un cero, habremos acabado moviendo el byte de esa posición un lugar a la derecha. Copiar un valor es un problema más complicado; asumiendo que las dos posiciones situadas a la derecha de la actual sean cero, se procederá de la siguiente forma: primero, usaremos [>+>+<<-], que tendrá el efecto de copiar el valor en la posición actual a la posición de su derecha y a la siguiente más a la derecha, y poner a cero la posición actual; después iremos dos posiciones a la derecha usando >>, tras lo cual usaremos una versión modificada del fragmento mover: [<<+>>-], es decir, mover el byte de la posición p (siendo p la posición del puntero de datos) a la posición p-2. Al terminar, retrocederemos otra vez dos posiciones usando <<, aunque dependiendo de la aplicación que queramos darle este último paso puede ser innecesario.

Si no estamos seguros de si están a cero las dos posiciones de la derecha de la actual, siempre podemos asegurarnos usando el siguiente fragmento: >[-]>[-]<<. Normalmente, sin embargo, no necesitaremos ejecutar este código, ya que estará a cero al comenzar.

Juntando todo esto, nos damos cuenta de que si al empezar tenemos en la posición p el valor a, en la posición p+1 el valor 0 y en la posición p+2 el valor 0, tras ejecutar el siguiente fragmento de código acabaremos teniendo en p el valor a, en p+1 el valor a, y en p+2 el valor 0:

[>+>+<<-]>>[<<+>>-]<<

¿Confuso? Considerando cada parte por separado, se ve claramente que simplemente estamos construyendo fragmentos cada vez más grandes mediante los bloques básicos que anteriormente hemos considerado.

Multiplicar un byte por una constante es sencillo: basta con utilizar el programa de mover, pero en lugar de incrementar una vez la variable de la derecha, la incrementamos tantas veces como haga falta. Por ejemplo, para multiplicar el byte actual por 7 podemos utilizar esto: [>+++++++<-], que deja el resultado a la derecha del byte actual, y éste a cero.

Multiplicar dos bytes entre sí requiere algo más de esfuerzo. La idea es sumar el segundo sobre el byte a su derecha tantas veces como diga el primero. Veamos cómo hacemos esto. Primero fijémonos en que la operación de copiar puede ser usada también para sumar, puesto que si el valor en la posición de la derecha de la actual no es cero, se le sumará el contenido del byte actual. Así pues, si llamamos c a la operación copiar, con este código resolveremos el problema: [>c<-], es decir, ir a la derecha, sumar el byte que hay allí al siguiente, ir a la izquierda, decrementar y continuar hasta que éste sea cero. Si se desea que no se pierda el primer multiplicando, habrá que empezar copiándolo a un lugar seguro.

El código completo queda así:

[>
  [>+>+<<-]
  >>
  [<<+>>-]
  <<
<-]

Veamos ahora un programa simple que imprime la «respuesta a la Gran Pregunta de la Vida, el Universo y Todo lo demás» (según Douglas Adams, escritor y humorista británico fallecido hace pocos años). Dicha respuesta es 42. El siguiente programa calcula el código ASCII del número 4 y lo imprime, y a continuación calcula el código ASCII del número 2 y lo imprime: +++++++[>+++++++<-]>+++.--.. El código ASCII del dígito 4 es 52 = 7×7+3, por tanto primero multiplicamos 7×7, y luego sumamos 3 al resultado y lo imprimimos. Después restamos 2 a lo que quedaba, ya que el código ASCII del dígito 2 es 50 = 52-2. Lo imprimimos, y ya lo tenemos.

Dejamos al cuidado del lector el resto del aprendizaje del lenguaje Brainfuck, para centrarnos en una forma de elaborar un intérprete de dicho lenguaje. Esta es una tarea realmente sencilla, como veremos enseguida; la única parte que presenta alguna complicación (poca, realmente) es llevar el balance de qué «]» corresponde con un «[» y viceversa. Precisamos de dos memorias, compuestas por sendos arrays (o arreglos, según algunos traductores): la de programa y la de datos, llamadas respectivamente mp y md. También necesitaremos dos variables: p y d, que serán los punteros de programa y datos, respectivamente.

He aquí un esquema del algoritmo principal del intérprete:

  Leer el programa en la memoria de programa, mp,
    guardando en la variable pfin la posición siguiente
    a la última usada, que indicará fin de programa.
  Poner a cero todos los elementos de la memoria de datos.
  Hacer p = 0, d = 0.
  Comienzo del bucle (1):
    Si p = pfin, fin de programa: ir a la etiqueta (4).
    Si la instrucción mp[p] es «-», hacer md[d] = md[d] - 1.
    Si la instrucción mp[p] es «+», hacer md[d] = md[d] + 1.
    Si la instrucción mp[p] es «<», hacer d = d - 1.
    Si la instrucción mp[p] es «>», hacer d = d + 1.
    Si la instrucción mp[p] es «,», leer un carácter y guardarlo en md[d].
    Si la instrucción mp[p] es «.», escribir el carácter que hay en md[d].
    Si la instrucción mp[p] es «[» y md[d] es cero, hacer lo siguiente:
      Hacer nivel = 0.
      Comienzo del bucle (2):
        Si mp[p] es «[», hacer nivel = nivel + 1.
        Si mp[p] es «]», hacer nivel = nivel - 1.
        Hacer p = p + 1.
        Si nivel = 0, ir al comienzo del bucle (1).
      Ir al comienzo del bucle (2).
    Si la instrucción mp[p] es «]», hacer lo siguiente:
      Hacer nivel = 1.
      Comienzo del bucle (3):
        Hacer p = p - 1.
        Si mp[p] es «]», hacer nivel = nivel + 1.
        Si mp[p] es «[», hacer nivel = nivel - 1.
        Si nivel = 0, ir al comienzo del bucle (1).
      Ir al comienzo del bucle (3).
    Hacer p = p + 1.
  Ir al comienzo del bucle (1).
  Etiqueta (4): fin de programa.

El intérprete recién descrito asume que los programas son sintácticamente correctos, es decir, que tienen un balance correcto de «[» y «]» y que el programa nunca utiliza la instrucción «<» cuando d = 0, ni la instrucción «>» cuando d está en la última posición disponible de md. También asume que el lenguaje efectúa correctamente el «salto» de 255 a 0 al incrementar, y de 0 a 255 en los decrementos. Si esto no fuera así, habrá que poner condiciones adicionales, convirtiéndose la operación de incrementar en la siguiente:

  Si md[d] = 255, hacer md[d] = 0; si no, hacer md[d] = md[d] + 1.

y la de decrementar, similarmente:

  Si md[d] = 0, hacer md[d] = 255; si no, hacer md[d] = md[d] - 1.

Durante el desarrollo de un programa Brainfuck es fácil equivocarse de forma que no cumpla los requisitos arriba expuestos. Para evitar sorpresas es aconsejable incluir en el intérprete comprobaciones en lugares estratégicos: comprobar antes de decrementar d que éste no es cero, y antes de incrementarlo que no está ya en el límite derecho; en los bucles que buscan el «[» y «]» correspondientes a su pareja, hay que comprobar que no llegamos a p = 0 o a p = pfin sin encontrar la pareja correspondiente, o en caso contrario detener la ejecución. Con esas precauciones el intérprete debería ser seguro frente a cualquier programa Brainfuck por mal construido que esté.

Ya para terminar, una pregunta: ¿cuál es la longitud del programa Brainfuck más corto capaz de escribir una o minúscula (código ASCII 111) dejando el resto de la memoria de datos con ceros?

Intérprete en JavaScript

El siguiente intérprete puede servir para probar código en Brainfuck. Incluye entrada y salida, pero no ejecución paso a paso ni visualización de los datos (véase la sección de enlaces para un depurador de Brainfuck más completo en C).

Programa:
Entrada:
Salida:
Ejecutar:

Enlaces

Por ahora la mayoría de las páginas enlazadas desde aquí están en inglés, ya que el tema parece que todavía no es muy conocido en nuestro país. Esperemos que con el tiempo la situación cambie.

Sobre lenguajes esotéricos en general

El lugar por excelencia donde encontrar información y referencias sobre lenguajes esotéricos es sin duda el Esoteric Languages Wiki:
http://www.esolangs.org/wiki/

Hay un índice de páginas apuntadas a un webring sobre lenguajes esotéricos, que también contiene multitud de referencias:
http://b.webring.com/hub?ring=esolang

Una excelente página dedicada a los lenguajes experimentales, mantenida por Chris Pressey:
Cat's Eye, http://catseye.tc/
Es de destacar la sección dedicada a los lenguajes de programación esotéricos:
http://catseye.tc/projects/eso.html

Eric S. Raymond es el autor de un compilador de INTERCAL, el C-INTERCAL. Su página llamada The Retrocomputing Museum contiene una selección de joyas del esoterismo en programación. Brainfuck tiene ocho instrucciones, pero ¿cuál es el mínimo número de instrucciones que debe tener un lenguaje para ser Turing-completo? ¡Una! Hay en esta página dos ejemplos, que llevan el concepto del RISC un paso más lejos: OISC (One Instruction Set Computing) y URISC (Ultimate RISC).
Otra de las joyas presentes en este museo es el kvikkalkul, un lenguaje pretendidamente utilizado en los submarinos nucleares suecos en la década de 1950, aunque más probablemente sea una broma. El lenguaje sólo soporta números en coma flotante sin parte entera, es decir, menores que 1.
También destacamos el MIXAL, que es el lenguaje ensamblador del procesador MIX de Knuth, mencionado en el texto, y un lenguaje de programación Klingon llamado var'aq. Hay muchas otras perlas que invitamos a descubrir.
http://www.catb.org/esr/retro/

La Enciclopedia de Lenguajes Estúpidos contiene una lista bastante exhaustiva de lenguajes esotéricos, sus características, el nombre de su creador, el año de creación y la página principal. Varios de los enlaces disponibles aquí han sido obtenidos gracias a esa página.
http://www.kraml.at/stupid/

Listas de correo relacionados con lenguajes esotéricos:
Archivo de la lista de correo de Cat's Eye

Selección de lenguajes esotéricos concretos

El lenguaje Whenever, cuyas instrucciones no se ejecutan en un orden preestablecido sino aleatorio:
http://www.dangermouse.net/esoteric/whenever.html

Las instrucciones del lenguaje Wierd son cambios de dirección en cadenas de símbolos. Esta es la especificación del lenguaje:
http://catseye.tc/projects/wierd/doc/wierdspec.txt

El lenguaje Piet mencionado en el texto, cuyas instrucciones son colores:
http://www.dangermouse.net/esoteric/piet.html

Descripción del lenguaje nihilista Sartre, creado por J. Colagioia, otro lenguaje pensado con buen humor. Es bastante llamativa la definición de la instrucción condicional IF.
http://catseye.tc/projects/sartre/doc/sartre.html

Sobre Brainfuck

He aquí un intérprete y depurador de Brainfuck escrito por el autor de este artículo (en inglés), suministrado en forma de código fuente en C. El código debería ser sumamente portable; compila perfectamente con gcc tanto en Windows como en Linux. El intérprete, además, realiza primero una pasada de optimización del código para que se ejecute más rápido. El depurador contiene funciones avanzadas que hasta ahora no he encontrado en ningún programa similar.
brfd101.zip (11.077 bytes)

Una completa guía acerca de los bloques con los que construir programas en Brainfuck:
http://home.planet.nl/~faase009/Ha_bf_intro.html

La demostración formal de que Brainfuck es Turing-completo:
http://home.planet.nl/~faase009/Ha_bf_Turing.html

Un intérprete de Brainfuck disponible en línea, escrito en JavaScript:
http://home.planet.nl/~faase009/Ha_bf_online.html

Propuestas de normalización del Brainfuck:
http://www.muppetlabs.com/~breadbox/bf/standards.html
y otra con cierto sentido del humor:
http://esoteric.sange.fi/ENSI/brainfuck-1.0.txt

Existen numerosos programas escritos en lenguaje Brainfuck; entre ellos destacamos un programa para averiguar si un número es primo, varios intérpretes y compiladores de Brainfuck escritos precisamente en Brainfuck, y un programa para calcular PI, aunque éste último requiere una extensión del lenguaje que permita que cada celda pueda almacenar números de 16 bits en vez de 8.

He aquí una biblioteca de programas escritos en Brainfuck. Destacamos el programa SORT.BF, que lee una entrada, la ordena mediante el método de la burbuja e imprime el resultado.
http://esoteric.sange.fi/brainfuck/bf-source/prog/

Otros enlaces indirectamente relacionados con lenguajes esotéricos

Una colección del programa Hello, World escrito en gran variedad de lenguajes, incluyendo muchos esotéricos, entre ellos BrainFuck e INTERCAL:
http://www.latech.edu/~acm/HelloWorld.shtml

99 Bottles of Beer es una canción popular inglesa y estadounidense, al estilo de la canción popular española cuya letra empieza así: Un elefante se balanceaba sobre la tela de una araña... La versión en inglés requiere contar del 99 al cero durante la canción. Escribir su letra es un ejercicio de programación indudablemente más complicado que el de Hello, World, ya que requiere un bucle finito, una cuenta atrás e imprimir números, y por ello los programas tienden a ser más largos pero a la vez más interesantes. He aquí una página dedicada a los programas que imprimen la letra completa de la canción 99 Bottles of Beer en diferentes lenguajes de programación; destacamos el escrito en A+ ya que es capaz de imprimir las versiones europea y americana. Por supuesto no faltan versiones Brainfuck ni INTERCAL del programa, e incluso una en Malbolge.
http://www.99-bottles-of-beer.net/

Los quines son programas capaces de reproducirse a sí mismos. No tienen, sin embargo, nada que ver con los virus: a diferencia de éstos, el requisito que han de cumplir los quines es que la salida del programa sea su propio código fuente, sin utilizar ningún fichero externo. Pensando un poco sobre el tema vemos enseguida que la tarea no es trivial, y que se parece al problema del huevo o la gallina. Hay ejemplos en muchos lenguajes, entre ellos INTERCAL y Brainfuck.
http://www.nyx.net/~gthompso/quine.htm

Lista exhaustiva de lenguajes de programación, antiguos y modernos:
http://ftp.wustl.edu/doc/misc/lang-list.txt

La Galería de los Descifradores CSS es una página creada para defender que un programa de ordenador puede ser acogido dentro de la ley de libertad de expresión, ya que al parecer un juez estadounidense declaró ilegal un programa escrito en lenguaje C que descifraba los sectores encriptados de los discos DVD, que utilizan un sistema criptográfico denominado CSS. Hay ejemplos en muchos otros lenguajes (entre ellos, cómo no, Brainfuck), y otras muchas formas de expresar el programa original: versiones recitadas del programa en formato MP3, descripciones detalladas del algoritmo paso a paso que pueden ser utilizadas para rehacerlo, y muchas otras divertidas maneras de convertir el algoritmo a formas que sí están claramente protegidas por la libertad de expresión. Dando vueltas a la tuerca, lleva el tema a extremos que rayan el ridículo, como la existencia de números primos ilegales.
http://www.cs.cmu.edu/~dst/DeCSS/Gallery/

Me faltan palabras. El diccionario de la Real Academia Española incluye incremento y decremento, así como incrementar, pero no decrementar.

Fraccionar archivos usando Reed-Solomon

Hace tiempo que necesitaba una utilidad capaz de dividir un archivo en varias partes. Pero no que hiciera sólo eso, que para eso ya existen muchas (Hacha, por ejemplo), sino una tal que si se pierden algunas partes (con un valor máximo de «algunas» decidido de antemano) todavía se pueda recuperar el archivo original.

El uso que le quería dar es una copia de seguridad distribuida. Se divide el archivo que se quiere guardar en múltiples partes y se suben a diferentes lugares: MediaFire, MegaUpload, FileFactory, 4shared, ADrive... debidamente cifradas de antemano si queremos preservar nuestra intimidad, claro. Si a la hora de recuperar las partes hay alguno de los servicios que ha cerrado, o que ha borrado el archivo, o cuya clave no nos funciona por alguna razón, siempre es posible reconstruir el original usando los demás, suponiendo que el número de bajas no sea excesivo.

La solución obvia es subir el archivo completo a cada uno de los alojamientos remotos. El problema está en el tamaño máximo soportado por cada alojamiento y en el ancho de banda total que hay que usar para subir tantas veces el mismo archivo.

Esto sugiere una pregunta: ¿Es posible obtener, a partir de un archivo dado, n+m archivos, de manera que si de ellas se pierden m partes cualesquiera, se pueda reconstruir el archivo original?

Sí, se puede, y además de forma óptima, es decir, que si el archivo tiene B bytes, el tamaño de cada bloque sería exactamente B/n si B es múltiplo de n. Si no lo es, no importa: nos guardamos la longitud original del archivo y añadimos bytes (por ejemplo, ceros) hasta llegar al siguiente múltiplo de n. Después, tras reconstruirlo, truncamos el archivo por su longitud original.

De hecho, el principio para hacerlo es el que se emplea en el RAID. No me refiero a la marca de insecticida, sino a un sistema genérico para agrupar varios discos (Redundant Array of Inexpensive —o Independent— Disks).

Según la forma de usar los discos, existen varios tipos de RAID, a los que se les asigna números. Algunos de esos tipos contienen información redundante para prevenir fallos de las unidades de disco. Los más básicos son RAID 1, RAID 3 y RAID 6. RAID 1 es el sistema más obvio: todos los discos tienen el mismo contenido. Es como la idea de subir el mismo archivo a todas partes. RAID 3 lo hace mejor: si hay N discos, la capacidad efectiva es N-1, y si se estropea uno, se puede reconstruir a partir de los demás. El sistema que emplea es muy sencillo: cada bit del disco extra es el XOR de todos los demás. Así, si R, S y T son los discos que contienen los datos normales, el disco U contiene R⊕S⊕T. Si se estropea R, se puede recuperar su contenido calculando S⊕T⊕U, ya que puesto que U=R⊕S⊕T, S⊕T⊕U = S⊕T⊕(R⊕S⊕T) = (quitando paréntesis y reordenando) S⊕S⊕T⊕T⊕R = 0⊕0⊕R = R. Lo mismo se aplica al resto de discos.

Sin embargo, no se puede extender el mismo truco a otro disco más y conseguir que si fallan dos discos cualesquiera, ambos se puedan recomponer. El truco del XOR está limitado a un disco fallido como máximo. Esto quiere decir que si falla un disco durante la recomposición de los datos originales (o hasta que se reemplaza el disco fallido), se pierden los datos. Para conseguir tolerancia a dos fallos o más, hace falta recurrir a los códigos Reed-Solomon. Esto es lo que hace el RAID 6.

No es trivial operar con estos códigos; hacen falta algunos conceptos de álgebra lineal y de estructuras algebraicas. Puesto que no encontré ningún programa ya hecho para dividir y recomponer datos, tuve que hacerme uno propio. Lo que sigue es una síntesis de lo que he averiguado durante su elaboración.

Hay un tutorial sobre códigos Reed-Solomon aplicados a sistemas RAID, aquí: [1] (PDF). La descripción de la matriz necesaria para generar los códigos (y su inversa para decodificarlos) es errónea; hay un artículo que la enmienda aquí: [2] (PDF).

Así que tenemos un archivo conceptualmente dividido en n bloques de datos, y queremos generar a partir de ellos un total de n+m bloques de datos, tales que si se pierden cualesquiera m de los n+m bloques, podamos reconstruir los que se han perdido. Para conseguirlo, dividiremos los bloques en palabras, es decir, conjuntos de bits de una longitud fija predeterminada w. El número de bits por palabra w es un valor escogido de tal forma que 2^w sea mayor que el máximo valor de n+m que vamos a emplear. Por ejemplo, si escogemos w=8 (por tanto las palabras son bytes), podremos dividir el archivo original en un máximo de 255 partes contando las que se pueden perder; por ejemplo, n=200, m=55.

Pero para empezar, supongamos que trabajamos en el dominio de los números reales; luego ya veremos cómo hacer lo mismo sólo con enteros de w bits. El problema consiste entonces en encontrar, a partir de una serie de datos d₁, d₂, ..., d_n, una serie de elementos c₁, c₂, ..., c_n+m que tengan la propiedad deseada. Veamos cómo hallarlos.

Dispondremos los datos en forma de una matriz columna, D. Para resolver el problema hemos de encontrar dos matrices A y B. La matriz A debe cumplir esta condición: que el producto AD sea una matriz columna C que contiene los elementos c₁, c₂, ..., c_n+m. La matriz B, por su parte, tiene que cumplir esta condición: si cogemos n elementos distintos cualesquiera de los n+m que tiene C y formamos con ellos una matriz columna C’, entonces BC’=D.

Si tenemos esas dos matrices A y B, el problema estará resuelto: si podemos usar A para calcular C, obtendremos c₁, c₂, ..., c_n+m y por tanto generar los bloques; si podemos usar B para calcular D a partir de cualquier subconjunto de n elementos distintos de C, podemos reconstruir los datos originales.

El problema, pues, radica en cómo construir las matrices A y B. Veamos la forma.

Para poder multiplicarla por D, la matriz A tiene que tener n columnas; para dar como resultado una matriz columna con n+m elementos, tiene que tener n+m filas. La característica que deseamos que tenga A, ya veremos después por qué, es que al tachar m filas cualesquiera, la matriz resultante sea siempre invertible (lo que equivale a requerir que su determinante no sea nulo). ¿Cómo lo conseguimos?

La respuesta viene de la mano de una familia de matrices llamadas matrices de Vandermonde. Estas matrices se construyen como sigue: sean a₁, a₂, ..., a_k escalares arbitrarios; entonces la fila i está compuesta por una sucesión geométrica que comienza en a_i⁰=1:

(Se define 0⁰=1 a este efecto). El determinante de una matriz cuadrada de Vandermonde nunca es cero si ninguno de los escalares está repetido (concretamente, su valor es ∏(a_j - a_i) para todos los posibles pares ordenados a_i, a_j de escalares que intervienen, que no será cero a menos que haya escalares repetidos), así que, si formamos una matriz rectangular de Vandermonde más alta que ancha con todos los escalares distintos, entonces al tachar cualesquiera filas que la hagan cuadrada, el determinante de la matriz resultante no será cero.

De modo que ese es el truco para construir nuestra matriz A: como una matriz de Vandermonde. Usaremos como escalares los números de fila empezando en cero, y se elevarán a los números de columna empezando en cero. La primera fila será pues: 0⁰=1, 0¹=0, 0²=0, ..., 0^n-1=0; la segunda será 1⁰=1, 1¹=1, 1²=1, ..., 1^n-1=1; la tercera será 2⁰=1, 2¹=2, 2²=4, 2³=8, ..., 2^n-1, etcétera. Todas sus submatrices cuadradas de orden n serán entonces invertibles, que es la propiedad que buscábamos.

Ahora veamos cómo construir B para reconstruir los datos originales a partir de C’, que como hemos dicho, es un subconjunto de n elementos de C. Está claro que B tiene que ser una matriz cuadrada de orden n, ya que al multiplicarla por C’, que tiene n elementos, tiene que darnos D, que también tiene n elementos.

Fijemos nuestra atención por un momento en cómo se construye la matriz C. Cada elemento c_i es el producto de la fila i de A por la única columna de D. Construyamos ahora una matriz A’ cuyas filas sean únicamente aquellas filas de A cuyo índice i coincide con el correspondiente de cada elemento c_i en C’. Es decir, construyamos A’ de tal manera que se cumpla la relación A’D=C’.

Entonces ahora es obvio que para hallar D, basta con invertir la matriz A’ puesto que A’^-1A’D=A’^-1C’, luego D=A’^-1C’, por tanto la matriz B buscada es simplemente A’^-1. Sabemos además que A’ es invertible porque la hemos construido así a propósito.

Recapitulando lo que llevamos hasta ahora, se trata de construir un par de matrices A y B tales que al tachar cualesquiera m filas de A, la submatriz resultante siga siendo invertible; para reconstruir los datos a partir de un subconjunto C’ de n bloques de los n+m que hemos generado, construimos A’ como la submatriz de A resultante de dejar únicamente las filas que se corresponden con las presentes en C’, y al invertirla obtenemos B.

Veamos un ejemplo. Tomemos n=3 y m=2. Tenemos tres datos d₁, d₂ y d₃ a partir de los cuales queremos obtener cinco elementos c₁, c₂, c₃, c₄ y c₅. Construimos primero la matriz A y la usamos para obtener los bloques:

Ahora supongamos que sólo tenemos los bloques 1, 3 y 5 y nos faltan los bloques 2 y 4, y queremos reconstruir los datos d₁, d₂ y d₃. Construimos la matriz C’ que consta simplemente de c₁, c₃ y c₅ y construimos también A’, usando las filas 1, 3 y 5 de A, la invertimos y la multiplicamos por C’ para obtener D:

Como cortesía adicional, podemos refinar la matriz A para que cada c_i para i entre 1 y n sea igual a d_i. Para ello, se pueden convertir las n primeras filas de A en una matriz identidad mediante transformaciones elementales, que son unas transformaciones que no afectan a la invertibilidad de la matriz. El algoritmo a aplicar, que también nos sirve para invertir la matriz, se llama algoritmo de Gauss-Jordan. Está explicado en la referencia [2].

Muy bien, muy bonito, pero estamos trabajando con reales de tamaño arbitrario, no con enteros de w bits. ¿Cómo hacemos para que no nos aparezcan números racionales o demasiado grandes?

Los cuerpos de Galois

Un cuerpo finito o de Galois (abreviado GF) es un cuerpo con un número de elementos finito. Hasta aquí, obvio. El más simple es GF(2) que tiene dos elementos, llamémosles 0 y 1. En ese cuerpo, la suma se define igual que en la aritmética en módulo dos (es decir, equivale a la operación XOR) y el producto es el aritmético habitual, que al ser realizado sólo con los elementos 0 y 1, equivale a la operación AND.

Como curiosidad, existen cuerpos de Galois de orden primo y de orden la potencia de un primo, pero no de ningún otro. Por ejemplo, no existen cuerpos de Galois de orden 6, porque 6 no es primo ni es la potencia de un primo, pero sí de orden 9, porque 9 = 3² y 3 es primo. Para construir un cuerpo de Galois de orden primo p (como el caso p = 2 recién nombrado), se puede usar la aritmética en módulo p. Sin embargo, la adición y la multiplicación módulo pⁱ para i > 1 no forman un cuerpo, por lo que hay que emplear otro sistema para construirlo.

Para crear cuerpos de Galois de orden 2^w, se usan como elementos polinomios de grado w con coeficientes en GF(2), es decir, los coeficientes pueden ser sólo 0 y 1, y al operar entre ellos se aplican las reglas de GF(2). La suma es entonces suma de polinomios, pero al ser los coeficientes de GF(2), al sumar o restar dos coeficientes se hace en realidad un XOR entre ellos. El producto es... bueno, el producto es un dolor de muelas. Para calcularlo hay que hallar el producto de los polinomios, módulo un polinomio especial llamado generador, característico del cuerpo con el que estamos trabajando.

Para traducir los polinomios a números enteros, se guarda el coeficiente del término de grado i en el bit i del número. Así, por ejemplo, el polinomio x²+1 en GF(2⁴) se almacena en un entero con el valor binario 0101, es decir, el valor decimal 5. Para sumar (o restar) dos elementos del cuerpo, basta entonces con hacer el XOR bit a bit. En la práctica, para multiplicar de forma eficiente se usan una tabla de logaritmos y una de antilogaritmos, es decir, a*b=antilog(log(a)+log(b)), considerando a=0 y b=0 como casos especiales. La división se traduce igualmente como el antilogaritmo de la resta de logaritmos. (Esa suma y esa resta concretas se hacen en aritmética convencional módulo 2^w-1).

Lo más interesante es que las propiedades de las matrices con las que aquí trabajamos se mantienen cuando operamos en GF(2^w), con tal de que 2^w sea mayor que el número de filas y de columnas de la matriz. Esto nos permite trabajar todo el tiempo con enteros mientras las operaciones las realicemos en el cuerpo. Obsérvese que el RAID 3 equivale a trabajar con w=1 y construir la matriz A de la siguiente forma: las n primeras filas forman una submatriz identidad, y la fila n+1 consiste en todo unos. Aunque en ese caso no se cumple que 2^w > n+m, sí que se cumple que todas las submatrices de orden n de A son invertibles, que es el requisito principal.

El programa

Con todos esos datos ya se puede realizar un programa como el que yo requería. He escogido w=8 porque, además de trabajar con bytes, que es rápido, existe el problema de que el algoritmo de Gauss-Jordan es de orden O(n³) y el almacenamiento de las matrices requiere O(n²). Si hubiera escogido w=16, la matriz requeriría un mínimo de 8 Gb de memoria para almacenarla completa y el algoritmo de Gauss-Jordan prefiero no pensar cuántas operaciones requeriría. Con w=8, la matriz necesita a lo sumo 64 Kb y en el peor caso Gauss-Jordan requiere del orden de 8 millones de operaciones. El inconveniente es que no se puede dividir el archivo en más de 255 partes en total, pero era una solución de compromiso necesaria. De todas formas, para mis propósitos es suficiente. El polinomio generador que he usado es el que viene en el tutorial para w=8, o sea, x⁸ + x⁴ + x³ + x² + 1.

He probado a dividir un archivo de 4,4 Gb en 255 partes de las cuales 8 se podían perder. Lo he reconstruido tras quitar ocho partes elegidas a dedo. El resultado coincidía con el original tal y como se esperaba.

Aún no he decidido la licencia (probablemente será GPL2 o GPL3), y está pendiente de una limpieza para hacerlo presentable. Si hay demanda, tal vez lo haga público. ¿Alguien más quiere el programa?

Referencias

[1] http://www.cs.utk.edu/~plank/plank/papers/CS-96-332.pdf
[2] http://www.cs.utk.edu/~plank/plank/papers/CS-03-504.pdf

¡Feliz aniversario, Newton!

Ditto.

Civilización en el cráter Hale

Hay un mito reciente circulando por la red que hace referencia a la posibilidad de que ciertas imágenes capturadas por la sonda Mars Express de la ESA representen en realidad signos de civilización [1] [2] [3] [4].

La controversia está causada por una confusión de quienes buscan inspirar sus fantasías en esas imágenes. El argumento principal es que, puesto que los mismos patrones se pueden ver en varias imágenes en diferentes posiciones, están necesariamente sobre la superficie de Marte y no son, por tanto, defectos en la captura de la imagen.

La imagen del vídeo [2] no se encuentra ya en la página que el autor indica, así que aquí hay un enlace directo: http://www.esa.int/esa-mmg/mmg.pl?idf=SEMPMT0A90E. Es una imagen de 2283×1522 píxels con este aspecto:

Crater Hale in perspective, looking west
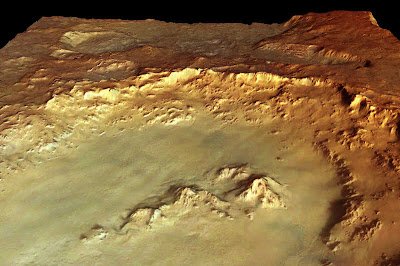
Credits: ESA/DLR/FU Berlin (G. Neukum)

No confíe el lector en la versión aquí replicada para análisis alguno, puesto que esta imagen está reducida y comprimida, y en los detalles pequeños, de los cuales aquí se han perdido muchos, radica la cuestión. Descargue la versión original de la web de la ESA si desea seguir este texto.

Aquí ya salta claramente a la vista un aspecto. O Marte es pequeñito y cuadrado, o esa imagen es un render en tres dimensiones usando un mapa de elevación y una textura. La descripción de la imagen dice así:

This perspective view, taken by the High Resolution Stereo Camera (HRSC) on board ESA's Mars Express spacecraft, shows Crater Hale on Mars.

The image is centred at latitude 36° South and longitude 324° East. The image was taken with a ground resolution of about 40 metres per pixel during Mars Express orbit 533 in June 2004. [...]

Esto es un error de la ESA, pues esa descripción, tal y como está escrita, da a pensar que esa imagen que se ve es directamente la captura de la sonda, cuando en realidad no es así: es la proyección en tres dimensiones de la misma utilizando un mapa de altura. La textura es casi con toda probabilidad esta: http://www.esa.int/esa-mmg/mmg.pl?idf=SEMTQWWJD1E y es la imagen de referencia que vamos a tomar en el siguiente análisis. Los datos de elevación para obtener el mapa de altura han sido obtenidos a partir de una versión estereoscópica capturada por la sonda, tal que esta: http://www.esa.int/esa-mmg/mmg.pl?idf=SEM1QWWJD1E.

De modo que los «analistas» toman imágenes que se ven en varias perspectivas, amplían la misma zona y en todas les aparecen los mismos patrones geométricos. Al hacerlo, no se dan cuenta de que están todo el tiempo observando la misma imagen aplicada como textura al mismo mapa de elevación colocado en diversas posiciones para hacer el render 3D.

Aquí vemos un detalle de estos patrones, sobre la imagen en perspectiva (recorte tomado tal cual de las coordenadas 1226,0 - 1522,446):

Y aquí vemos la misma zona de la imagen original (tomada de las coordenadas 1300,40 - 1450,190; después girada 180° para que la posición coincida con la anterior, después ampliada un 300% y por último aplicando el filtro Normalize de GIMP, aunque con cualquier método de aumento del contraste se apreciará el cuadriculado igualmente):

Se puede observar que, efectivamente, los patrones cuadriculados coinciden para la vista en perspectiva y para la imagen original. Lógico, es la misma imagen, con el contraste aumentado en la vista en perspectiva debido a la iluminación 3D. Más de uno estará sin duda preguntándose, a la vista de las imágenes, por qué tanto revuelo por unos artefactos JPEG. Es una buena pregunta que cabría dirigir a los proponentes de estas ideas. Para los que no, van unas explicaciones. El análisis es extensible a todas las porciones que muestran «signos de civilización», pero nos centraremos en el recorte recién presentado.

Funcionamiento de la cámara

La Cámara Estéreo de Alta Resolución (HRSC, por sus siglas en inglés) es una cámara que registra la imagen línea a línea de barrido, a diferencia de las cámaras convencionales que registran la imagen completa cada vez. Cada línea contiene 5.184 píxels; la altura no depende de la resolución de la cámara, sino que es indefinida. La frecuencia de los barridos depende de la velocidad de movimiento de la sonda, para hacer coincidir los tamaños horizontal y vertical. Se toman nueve canales simultáneamente: tres de RGB, tres de datos tridimensionales, uno del infrarrojo cercano y dos de fotometría. Hay más información sobre la cámara aquí: HRSC on Mars Express.

Para poder transmitir a la Tierra la ingente cantidad de datos generada por la cámara, fue preciso hacer algunas concesiones. Concretamente, hubo que reducir en algunos casos el número de pixels y que comprimir mediante JPEG, buscando un compromiso entre la calidad de la imagen y el ancho de banda de la transmisión. Aun con esas reducciones, la cantidad de datos transmitida está en el orden de los terabytes. Lo fundamental aquí es que la versión que llega a la Tierra ya está comprimida con JPEG. Aunque en la galería se presenten archivos TIFF comprimidos sin pérdida, las imágenes que contienen ya han pasado por una compresión JPEG en su transmisión a la Tierra.

Algoritmo de compresión

Conceptualmente, la compresión JPEG funciona, a grandes rasgos, como sigue. Se divide la imagen en cuadrados de 8x8 píxels (los bordes necesitan tratamiento especial si la resolución de la imágen no es múltiplo de 8). Para cada cuadrado, se realiza una transformada discreta del coseno (DCT), lo que se traduce en la práctica en descomponer el cuadrado en una combinación lineal de estos cuadrados:

Cuadros de la transformada discreta del coseno usada en la compresión JPEG. Imagen generada mediante un programa en PHP listado en un apéndice al final de la entrada.

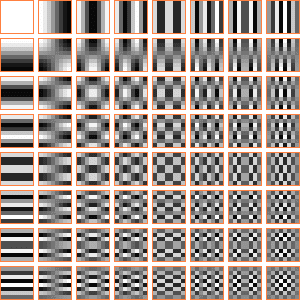
Es decir, se descompone como la suma del primer cuadro multiplicado por un número, más el segundo multiplicado por otro número, más el tercero multiplicado por otro... En total, sesenta y cuatro coeficientes. Esos coeficientes (que pueden ser negativos) son los que en realidad se guardan, en lugar de los píxels. Después es posible reconstruir el cuadrado original a partir de esos sesenta y cuatro valores. La compresión se consigue reduciendo la precisión con que se almacenan. En realidad, lo que se guarda son unos números enteros que representan los coeficientes con la precisión reducida. Se almacenan, además, en formato comprimido (típicamente Huffman), pudiendo llegar a ocupar cada uno incluso tan poco como un bit.

Además de esto, en las imágenes en color también hay un cambio de espacio de color, de RGB a YCbCr, para codificar la luminancia y la crominancia de forma distinta, puesto que el ojo es más sensible a los cambios de iluminación que a los de color. Así, la crominancia se codifica en píxels más «gordos» o más «anchos» que la luminancia, lo que implica menos información que comprimir. A este proceso se le llama downsampling (reducción de muestreo) de la crominancia.

Esa es la base de la teoría. Si hay alguien interesado, existen explicaciones más detalladas en [5], [6], [7] y [8], por ejemplo (la última incluye además código Haskell para decodificar un JPEG simple monocromo).

Dependiendo de multitud de factores, es posible que en el proceso de compresión queden muchos de los cuadros anulados (coeficiente cero) y tan sólo se vean uno o dos sumados. Además, cuando la diferencia de tonalidad de una zona es escasa, el rango dinámico es bajo y las variaciones pueden verse reducidas incluso a dos tonos. Cuando esto ocurre, el efecto (amplificado a blanco y negro puros) es el representado en la siguiente figura:

O su inverso:

Comparemos de nuevo con la imagen marciana:

O los marcianos cultivan sus campos dándoles forma de cuadro de DCT, o esto tiene todo el aspecto de ser artefactos (efectos secundarios no deseados debidos a la pérdida por la compresión).

Desmontando excusas

Vamos a ir viendo y comentando las objeciones con las que me he encontrado.

Es que es la única zona fotografiada por la Mars Express en la que se dan esos defectos. Eso es porque a la ESA se les ha pasado censurarlo.

No. Es la única fotografía donde se ven a simple vista, pero los defectos están en más imágenes, aunque en la mayoría de las demás hay que saber cómo sacarlos a relucir.

Ante todo, hay que tener en cuenta que esa no es la imagen tal como la tomó la sonda, como más adelante veremos, sino una versión postprocesada para hacerla más brillante y mejorar el contraste. Esa mejora del contraste es la que hace que los defectos salgan a la luz. Eso es aún más notable en la versión 3D.

Un ejemplo donde se ven defectos similares:

«Echus Chasma, nadir view», obtenido de http://www.esa.int/esa-mmg/mmg.pl?idf=SEMG9GSHKHF, mostrando en un recuadro la región recortada a continuación. Credits: ESA/ DLR/ FU Berlin (G. Neukum).

Echus Chasma, fragmento ampliado de la versión TIF en alta resolución, comprimido sin pérdida y sin ningún postprocesado. Coordenadas origen: (5920, 1200) - (6320, 1600).

A simple vista no se ven los mismos defectos, pero si descomponemos la imagen en YCbCr (el espacio de color en el que trabaja la compresión JPEG), obsérvese lo que aparece en el canal Cb:

Parece que se adivina algo. Mejoremos el contraste (usando Normalize):

Ahí están de nuevo. Obsérvese el tamaño de los puntos de la cuadrícula secundaria, mucho mayores que los píxels de la imagen. Esto nos indica que en esta imagen o se ha hecho un downsampling de crominancia enorme, probablemente de 6×6 u 8×8, o más probablemente, la ESA ha empleado la vista nadir para aportar datos de luminancia, ya que la resolución de dicha vista es sustancialmente mayor.

Pero has tenido que hacer malabarismos para sacar esos defectos a relucir. En la imagen original se ven a simple vista o simplemente aumentando un poco el contraste.

Es cierto que ha habido que hacer algunos malabarismos, pero no es cierto que en la imagen original se vean tan fácilmente. Sólo se ve en imágenes postprocesadas. Las siete que hay del Hale en la galería de imágenes de la ESA (a fecha de escritura de esta entrada) son postprocesadas y proceden de la misma imagen original.

¿Y cuál es la imagen original? Para averiguarlo tenemos que seguir las pistas indicadas en este breve artículo: [9]. Esto nos conduce a la web de la Freie Universität Berlin (FUB). Tienen un subdominio específico para el mapa de Marte elaborado por la Mars Express: http://hrscview.fu-berlin.de/. Buscamos una imagen que incluya el cráter Hale y la órbita Nº. 533, que es la nombrada en la descripción de la imagen que nos interesa.

Está aquí: [10].

Está disponible para descarga en dos formatos: PDS (alojado en el PSA, el Planetary Science Archive de la ESA) y VICAR (alojado en la propia FUB). Ninguno de los dos formatos es reconocido por Gimp directamente (aunque hay un plugin para leer PDS aquí: http://registry.gimp.org/node/1627), pero el VICAR tiene una estructura lo bastante sencilla como para que se pueda leer sin necesidad de conversores específicos. El ImageMagick que tengo viene con códec de VICAR, así que quien tenga la misma suerte puede usarlo para convertir los archivos a un formato reconocible por nuestro programa gráfico sin más. El xloadimage también soporta VICAR y también es capaz de realizar la conversión con el parámetro -dump. Nos interesan los canales rojo, verde y azul (los acabados en re4.53.bz2, gr4.53.bz2 y bl4.53.bz2, respectivamente).

Para los que no quieran instalarse el ImageMagick sólo para convertirlo, explicamos aquí cómo hacerlo de forma artesanal pero sencilla. El formato VICAR es muy simple: consta de una cabecera en ASCII y a continuación, los datos crudos de la imagen. En este caso todos los archivos son imágenes en escala de grises con 8 bits por píxel. Al no soportar compresión, han sido comprimidos con bzip2 para que ocupen menos. Los usuarios de Windows que no conozcan el bzip2 quizá puedan descomprimirlo con WinRar o WinZip.

Para convertir la imagen descomprimida a formato TGA, más popular, basta con descargar este archivo [11] y anteponerlo al VICAR, con lo que se convertirá en TGA. Para anteponer el archivo, el Linux y el Windows tienen formas diferentes de hacerlo. En Windows, en una ventana de símbolo del sistema, se puede escribir:

copy /b h0533_0000.tgahdr + h0533_0000.re4.53 h0533_0000.re4.53.tga
copy /b h0533_0000.tgahdr + h0533_0000.gr4.53 h0533_0000.gr4.53.tga
copy /b h0533_0000.tgahdr + h0533_0000.bl4.53 h0533_0000.bl4.53.tga

Y en Linux, en una ventana de terminal:

cat h0533_0000.tgahdr h0533_0000.re4.53 > h0533_0000.re4.53.tga
cat h0533_0000.tgahdr h0533_0000.gr4.53 > h0533_0000.gr4.53.tga
cat h0533_0000.tgahdr h0533_0000.bl4.53 > h0533_0000.bl4.53.tga

El archivo h0533_0000.tgahdr sirve sólo para imágenes con resolución 3512×19608, por lo que la única imagen adicional para la que servirá es para la infrarroja, por si alguien tiene curiosidad.

Tras añadir la cabecera TGA al archivo VICAR, hay que desechar las tres primeras líneas, ya que no son datos de imagen, sino de la cabecera VICAR, que todavía está en el archivo. De todas formas, la parte que nos interesa está cerca del límite inferior de la imagen. Es el último cráter grande visible, y está cortado por la derecha (por eso la imagen en la galería de la ESA también lo está).

Cada imagen TGA se puede usar como uno de los canales RGB para recomponer la imagen. En Gimp esto se puede hacer con Compose. Temporalmente (durante unas pocas semanas desde la fecha de escritura de esta entrada), la imagen resultante está disponible para descarga aquí: [temp1]. Ocupa 48 Mb comprimida como PNG. La versión descomprimida ocupa más de 200 Mb, así que es preferible que tengamos un ordenador con bastante memoria si queremos abrirla con un navegador. Los créditos de rigor:

HRSCview. Freie Universitaet Berlin and DLR Berlin, http://hrscview.fu-berlin.de/

Esta es «casi» la imagen original usada por la ESA para obtener la imagen principal del Hale de la galería. Aquí está la misma zona que en las imágenes anteriores, una vez recortada y rotada, con su color original y con los datos byte a byte coincidentes con los originales:

Es de destacar lo oscura que está, por lo que siendo datos de 8 bits, el rango dinámico está obviamente mermado. También está muy azulada; no hay apenas tonos rojizos. Nada comparable a ese cráter Hale brillante que se nos muestra en http://www.esa.int/esa-mmg/mmg.pl?idf=SEMTQWWJD1E.

Veamos su descomposición RGB (clic para ampliar):

Descomposición RGB del recorte original anterior (vista en rojo, verde y azul).

Para apreciar mejor los detalles, veamos lo mismo pero en escala de grises:

Descomposición RGB del recorte original anterior (vista en escala de grises).

Todavía no se ven muy bien, así que aquí va una versión con el contraste mejorado:

Versión con contraste mejorado de la imagen anterior.

Con esto ya podemos sacar algunas conclusiones. El canal R ha quedado prácticamente destrozado por los artefactos de compresión, al estar tan oscuro. El canal G y el B aún son un poco aprovechables. Comparemos ahora con la descomposición RGB de la imagen de la galería de la ESA:

Descomposición RGB del fragmento de interés de http://www.esa.int/esa-mmg/mmg.pl?idf=SEMTQWWJD1E.

El canal G y el B coinciden, sin duda, pero ¿de dónde ha salido ese canal R tan nítido comparado con la imagen VICAR?

La respuesta: del canal nadir. Sí, esa imagen con la friolera de 14048×78432 píxels y 354 Mb comprimidos (más de 1 Gb descomprimido) que hay para descarga. Abarca la misma área pero a mayor resolución. Concretamente, 4 veces más resolución en cada eje (es decir, 16 píxels por cada píxel de las otras).

He comprobado que coinciden. No puede generarse un TGA porque el tamaño vertical es mayor que el máximo admitido por dicho formato, que es 65.535, así que lo he convertido a PGM. Al Gimp le ha costado un rato cargar la imagen, otro rato hacer el recorte del cráter y otro rato cerrarla, pero al final obtuve mi premio, un recorte de 800×800 de la zona de interés (clic para la versión completa):

Recorte del canal nadir captado por la HRSC en la órbita 533 de la sonda Mars Express (original sin modificar).

Una vez escalada y ajustados los niveles, la coincidencia es casi total:

Comparación de la vista nadir (izquierda) con el canal R de la imagen de la ESA (derecha).

Las escasas diferencias se deben probablemente a pequeños ajustes del autor de la imagen de la galería para orientarla de acuerdo con una proyección nadir y hacerla coincidir con los canales G y B.

Y el canal G (verde) exhibe exactamente los mismos defectos que la imagen de la discordia:

Comparación de los defectos del canal G de la imagen original con los defectos de la imagen en perspectiva

En resumen, la imagen del cráter Hale usada como textura en los render 3D es una versión retocada, con color falso (en concreto, un canal rojo que no es el real sino que procede de la imagen nadir pancromática) de una imagen muy oscura y deteriorada de partida, en la que los defectos de compresión salen a la luz en cuanto se aumenta el contraste. Al usar la misma imagen para todas las proyecciones, los defectos han sido reproducidos de igual manera. Se aplica tanto a http://www.esa.int/esa-mmg/mmg.pl?idf=SEMPMT0A90E como a http://www.esa.int/esa-mmg/mmg.pl?idf=SEMCMT0A90E.

Si fuera como dices, se verían patrones similares en otras imágenes.

Sólo en las que han sido postprocesadas, amplificando los defectos sustancialmente. Como en esta imagen de Google Maps: [12]

¿Puedes acaso mostrar una del mismo cráter donde no se vean los mismos patrones?

Sí. Hay más imágenes del cráter Hale, como estas de la NASA: [13]

Pero esa es de la NASA y podrían haber sido más cuidadosos encubriendo. Además, esa imagen tiene menos resolución.

Bien, pues veamos más imágenes de la FUB que recogen el cráter Hale. La órbita 511: [14]. Puesto que ya hemos visto cómo extraerla, vamos al grano. Aquí una cabecera apropiada para una imagen con esa resolución: [15]. La imagen recompuesta (2294×14826, 28 Mb) está temporalmente disponible para descarga aquí: [temp2]. Se ve nuestra zona de interes por los pelos (la raya negra de arriba es el borde de la captura):

Recorte de la porción de interés de la imagen VICAR en [14].

La imagen es más clara, con lo cual hay mayor rango dinámico y la calidad por tanto es mejor, como se ve en la descomposición RGB siguiente, incluyendo el canal R, que, aunque deteriorado, al menos ya muestra algún detalle:

Descomposición RGB de la imagen anterior con los niveles ajustados.

Compárese con la descomposición RGB de la anterior, la correspondiente a la órbita 533:

¿Tiene defectos de compresión la 511? Sí, sin duda. ¿En los mismos lugares? Definitivamente no. Son imágenes distintas. Los patrones han cambiado de forma por completo, porque no eran sino defectos del JPEG.

Otras imágenes del cráter Hale que al lector le puede interesar estudiar: [16], [17].

Conclusiones finales

Los defectos de la compresión JPEG de la imagen tomada como origen para obtener las demás, eran demasiado acusados en el canal R como para poder usarlos, por lo que han sido descartados y reemplazados; los canales G y B se han mantenido, y sus defectos han trascendido a las imágenes finales, siendo los del canal G los más acusados y visibles. Otras tomas del mismo cráter no exhiben los mismos patrones, sino otros diferentes. Se trata pues, sin duda, de artefactos de compresión JPEG.

Y a modo de postdata, la imagen de la órbita 2526 procesada por el visor HRSCview, donde no se ve más que lo que hay, un cráter: 2526_0001.

Apéndice

A continuación se lista el programa en PHP para obtener la imagen con los cuadrados DCT del JPEG.

<?php
  // Resolución de color (Nº. de tonos de gris). Máx. 255.
  $r = 255;

  $img = imagecreate(300, 300);
  $clr = array();
  $bg = imagecolorallocate($img, 255, 128, 64); // Fondo
  $clr[0] = imagecolorallocate($img, 0, 0, 0);
  for ($i=2; $i<256; $i++) $clr[$i-1] = imagecolorallocate($img, $i, $i, $i);
  for ($yy = 0; $yy < 8; $yy++) {
    imagefilledrectangle($img, 0, 38*$yy+34, 299, 38*$yy+37, $clr[254]);
    imagefilledrectangle($img, 38*$yy+34, 0, 38*$yy+37, 299, $clr[254]);
    for ($xx = 0; $xx < 8; $xx++)
      for ($y = 0; $y < 8; $y++)
        for ($x = 0; $x < 8; $x++) {
          $c = (  cos((2*$x+1)*$xx*pi()/16)
                * cos((2*$y+1)*$yy*pi()/16) + 1.0) * 0.4999999;
          imagefilledrectangle($img, $xx*38+1+$x*4, $yy*38+1+$y*4,
                                     $xx*38+4+$x*4, $yy*38+4+$y*4,
                               $clr[floor($c*$r)*(254.9999999/($r-1))]);
        }
  }
  header('Content-type: image/png');
  imagepng($img);
  imagedestroy($img);
?>

Hay un color para los bordes y 255 grises. Para dar cabida al color de los bordes, se ha eliminado el color con RGB (1, 1, 1). El parámetro $r es la resolución de color, esto es, el número de colores (tonos de gris) que habrá en la imagen. Ajustándolo a 2 se obtiene la versión bicolor usada en el texto. Para obtener la imagen en negativo, cámbiese floor por 254-floor.

Agradecimientos

Agradecimientos a Julio por los datos que aportó en la discusión sobre este tema, especialmente algunos enlaces de los presentados.

También a la ESA, la FUB y el DLR (el Centro Aeroespacial Alemán) por hacer públicas las imágenes y los datos.

Referencias

[1] http://www.marsanomalyresearch.com/evidence-reports/2005/084/hale-civ-evidence.htm
[2] http://www.youtube.com/watch?v=qcR7VX-FwDY
[3] http://www.youtube.com/watch?v=PDEiHJwjCwc
[4] http://www.youtube.com/watch?v=0-dHqJYcDOM
[5] http://www.ams.org/featurecolumn/archive/image-compression.html
[6] http://dvd-hq.info/data_compression_2.php
[7] http://www.cs.sfu.ca/CC/365/mark/material/notes/Chap4/Chap4.2/Chap4.2.html
[8] http://www.imperialviolet.org/binary/jpeg/
[9] http://adsabs.harvard.edu/abs/2008LPI....39.1822M
[10] http://hrscview.fu-berlin.de/cgi-bin/ion-p?page=product.ion&code=25554104&image=0533_0000
[11] http://www.formauri.es/personal/pgimeno/xfiles/Hale/h0533_0000.tgahdr
[12] http://maps.google.com/maps?f=q&source=s_q&q=15%C2%B039%2702.89%22S+128%C2%B041%2751.78%22E&sll=37.0625,-95.677068&sspn=33.077336,63.369141&ie=UTF8&ll=-15.650674,128.69778&spn=0.002454,0.003868&t=h&z=18
[13] http://alderaan.arc.nasa.gov/pdsimages/select?qt=simple&q=product_id%3A%22611A46%22
[14] http://hrscview.fu-berlin.de/cgi-bin/ion-p?page=product.ion&code=78872241&image=0511_0000
[15] http://www.formauri.es/personal/pgimeno/xfiles/Hale/h0533_0000.tgahdr
[16] http://hrscview.fu-berlin.de/cgi-bin/ion-p?page=product.ion&code=79936214&image=2526_0001
[17] http://hrscview.fu-berlin.de/cgi-bin/ion-p?page=product.ion&code=99640167&image=4343_0000.

Actualización

La FUB confirma mis hallazgos: Respuesta de la FUB sobre las imágenes del Hale

Aproximando el círculo

Las curvas de Bézier son una construcción geométrica muy útil usada en multitud de ámbitos, especialmente en los relacionados con el dibujo. Fueron desarrolladas por el físico y matemático francés Paul de Faget de Casteljau mientras trabajaba para Citroën, y popularizadas y patentadas por el ingeniero francés Pierre Étienne Bézier durante su trabajo en Renault. Son segmentos de ciertas curvas paramétricas, cuyo parámetro se halla entre 0 y 1. Las más comunes son las cuadráticas (usadas sobre todo en fuentes TTF) y las cúbicas (usadas en casi todos los programas de dibujo vectorial y en lenguajes gráficos como el PostScript). Las cuadráticas requieren un punto extra, además del punto origen y el destino, y las cúbicas dos puntos extra. Tienen muchas propiedades atractivas para el dibujo; por ejemplo, que en los extremos son tangentes a las líneas que van desde los mismos hasta los puntos de control inmediatos, lo cual permite encadenarlas para formar curvas más largas sin aparentes ángulos, o que es sencillo subdividir un segmento dado en un punto arbitrario del mismo para obtener dos segmentos.

Existe una interpretación geométrica sencilla para la curva de Bézier de grado n. Phil Tregoning creó las siguientes imágenes casi autoexplicativas sobre la interpretación geométrica de las curvas de Bézier, en este caso la cuadrática y la cúbica:

(Fuente: Wikpedia).

Para la cuadrática, por ejemplo, primero se hace una interpolación lineal del segmento P₀P₁ entre 0 y 1 según el parámetro t, y luego se hace lo mismo con el segmento P₁P₂. Los dos puntos hallados determinan un tercer segmento, que al interpolarlo entre 0 y 1 según t, da un punto de la curva. La cúbica requiere seis interpolaciones lineales: los tres segmentos P₀P₁, P₁P₂ y P₂P₃, los dos segmentos intermedios obtenidos con las interpolaciones anteriores, y el segmento final.

Las ecuaciones paramétricas de la curva cuadrática y de la cúbica son relativamente sencillas:

B²(t) = P₀ (1-t)² + 2 P₁ t (1-t) + P₂ t²
B³(t) = P₀ (1-t)³ + 3 P₁ t (1-t)² + 3 P₂ t² (1-t) + P₃ t³

Es posible convertir una curva cuadrática en cúbica. Para hacerlo, hemos de tomar puntos P₁ y P₂ estratégicamente; concretamente, si Q₀, Q₁ y Q₂ son los puntos que definen la curva cuadrática, hay que escoger P₁ de forma que esté a 2/3 del camino entre Q₀ y Q₁, y P₂ de forma que esté a 2/3 del camino entre Q₂ y Q₁, y, por supuesto, P₀ = Q₀ y P₃ = Q₂. La curva cúbica resultante coincide en todos sus puntos con la cuadrática.

Como es de esperar, lo contrario no es posible en general: no se puede obtener una curva cuadrática que coincida con una cúbica. Lo que sí se puede hacer es aproximarla, usando más de un segmento de curva cuadrática.

Y es que las curvas de Bézier son en realidad muy útiles para aproximar figuras. Un caso particular donde se usan curvas de Bézier para aproximar una figura es el de los círculos. Con la cantidad suficiente de segmentos de curva de Bézier cúbica, es posible hallar una aproximación más que decente a una circunferencia.

Tres segmentos son definitivamente insuficientes; el resultado es demasiado deforme. Sin embargo, con cuatro segmentos basta para obtener una excelente aproximación; tan buena, de hecho, que muchos programas de dibujo vectoriales implementan sus círculos internamente mediante curvas de Bézier, en lugar de usar genuinos círculos. Entre los que lo hacen están Inkscape, Skencil (antes Sketch) y Sodipodi (del que salió Inkscape), tres conocidos programas libres de dibujo vectorial.

Si aplicamos una transformación afín a los puntos de control (P₀...P_n) de una curva de Bézier, el resultado que obtenemos es equivalente a transformar cada punto de la curva. Esta deseable propiedad nos permite usarlas para obtener la aproximación de una elipse en lugar de la de una circunferencia.

Para obtener la aproximación de un cuarto de circunferencia, hay que colocar los cuatro puntos de la forma que sigue. Supondremos que se trata de aproximar un círculo de radio unidad centrado en el origen; los demás se pueden obtener fácilmente escalando y desplazando puntos.

El primer punto, P₀, hay que situarlo en (0, 1); el segundo punto, P₁, en (k, 1) para cierto valor de k; el tercero, P₂, en (1, k) y el cuarto, P₃, en (1, 0). Con esto se aproxima un cuarto de circunferencia. Los demás segmentos se obtienen fácilmente por simetría y traslación.

¿Qué valor de k es apropiado? Hay quien sugiere usar k=4/3 (2^½-1) ~= 0,552284749...; este valor está calculado para que cuando t = 1/2, el punto de la curva resultante esté a distancia 1 del centro, de modo que coincida con el que se le supone a una circunferencia.

Sin embargo, ese valor tiene sus desventajas: en casi todos los puntos, el círculo aproximado resultante es ligeramente más grande que el real, lo que determina que su área sea también más grande. En concreto, el área excede la teórica del círculo en aproximadamente un 0,028%. No es mucha la diferencia, pero si se es un perfeccionista como algunos de nosotros, molesta. ;)

El área de nuestro segmento de Bézier (véase por ejemplo Paul's Online Math Notes - Area with Parametric Equations sobre cómo obtenerla) es A = 1/2 + 3/5 k - 3/20 k². Si la igualamos a π/4 y resolvemos k, obtendremos el valor de k que hace que el área coincida con la del círculo. El valor resulta ser k = 2 - (22/3 - 5/3 π)^½ ~= 0,551778477... (la otra solución da k > 1, que no nos interesa).

Este último valor de k da una curva que cruza varias veces el círculo, por lo que la distancia es menor dando al mismo tiempo una distancia ligeramente más pequeña, y en general es una aproximación mejor.

No es que se vaya a notar mucho la diferencia, todo sea dicho. Por ejemplo, el Inkscape usa k = 0,552 y no me había percatado de ello hasta que he mirado el código para escribir este texto. Pero, vaya, al menos quien use el valor de k sugerido aquí podrá tener la conciencia tranquila de que sus círculos son la mejor aproximación posible a un círculo real.

Actualización a 11 de diciembre

Ese valor de k que iguala las áreas tiene un pequeño problema. Aunque el área sea correcta, la distancia a una circunferencia real es casi la misma que con el valor de 4/3(2^½-1), sólo ligeramente menor. En particular, con el valor que iguala áreas es de 0,0002684... mientras que con el que iguala el punto medio es de 0,0002753...

El hecho de que cruce la circunferencia, por tanto, no constituye garantía por sí mismo de que la distancia sea menor, aunque esta vez haya habido suerte y haya sido así. He corregido esa parte de la entrada.

Y es posible reducir aún más esa distancia. Esta gráfica representa la distancia entre cada punto de la curva y la circunferencia de radio unidad, con t en el eje de abscisas, para tres valores de k (hemos ampliado la escala del eje de ordenadas para verla mejor):

El del centro es el que está usando Inkscape. Con k = 0,552 la distancia máxima resulta de sólo 0,000212..., que está más cerca de la circunferencia ideal. El valor de k que minimiza la distancia se obtiene de una ecuación polinómica de 6º grado que no voy a reproducir por ser bastante larga, que resulta en un valor de k ~= 0,55191502449...; la distancia máxima a la circunferencia ideal que se obtiene con dicho valor es 0,000196076...

Así que sólo nos queda decidir qué objetivo perseguimos. Si se trata de igualar el área, el valor de k que lo consigue es el de 0,551778...; si se trata de minimizar la distancia a la circunferencia verdadera, el valor es en cambio el de 0,551915... Elija veneno.