Colección de Simon Tatham: Range

Un nuevo puzle ha sido añadido a la colección de Simon Tatham. Se llama Range y es interesante. Las reglas pueden recordar un poco al Singles en algunos aspectos, pero en realidad al jugarlo encontramos reminiscencias del Pattern más bien.

Las reglas no están muy bien explicadas en la documentación, así que voy a dar una explicación aquí. Nos presentan un casillero con varios números colocados en varias casillas. Nuestro objetivo es determinar qué casillas hay que rellenar de negro, cumpliendo las siguientes reglas:

• Todas las casillas que no son negras tienen que formar una figura conexa, es decir, no se permite aislar una casilla blanca o un grupo conexo de casillas blancas en una «isla». Se entiende que están conectadas por arriba, abajo, izquierda o derecha; las diagonales no cuentan.
• No puede haber dos cuadrados negros adyacentes (igualmente, por arriba, abajo, izquierda o derecha).
• Las casillas con números no se pueden pintar de negro.
• Cada número indica la cantidad de casillas totales, incluida ella misma, que pueden alcanzarse hasta tropezar con una casilla negra, moviéndose hacia arriba, abajo, izquierda o derecha a partir de la casilla donde está el número.

Por ejemplo, en el tablero por defecto de 9×6, si aparece un 14, eso quiere decir que no hay ninguna casilla negra en la fila ni en la columna donde aparece dicho número, pues hay 8 casillas horizontales y 5 casillas verticales además de la propia casilla, en total 14. Si aparece un 13, quiere decir que hay una casilla negra en uno de los cuatro extremos, no sabemos en principio en cuál, y todas las demás son blancas.

En la documentación pone como ejemplo el número 1. Si apareciera un 1, al contarse a sí misma ya estaría el cupo lleno, por lo tanto ese 1 debería estar rodeado de casillas negras. Pero eso formaría una región de una casilla que estaría aislada del resto de casillas blancas, quebrantando otra de las reglas. Por lo tanto, no puede aparecer un 1 en ningún tablero.

Como ayuda para resolver los problemas, podemos marcar casillas con un punto que indica «esta casilla no es negra». Así, por ejemplo, en cuanto colocamos una casilla negra podemos rodearla de puntos para recordarnos que ahí no puden ir otras casillas negras, de acuerdo con las reglas.

Como de costumbre, la solución de cada problema es única. El grado de adicción lo compararía con el del Pattern también. Podría decirse que Range (Kurodoko) es a Pattern (Nonograms, Picross) como Unequal (Futoshiki) es a Solo (Sudoku).

Enhorabuena, acaban ustedes de sobrevivir a otro fin del mundo.

Batallitas

Las psicofonías son el arte de decirte lo que has de oír. Y es que, cuando te dicen lo que has de oír, lo oyes esté o no ahí. Un ejemplo:

(La canción está en Hindi, su título original es Mehboob Mere y pertenece a la película Fiza; la letra real en Hindi —o mejor dicho, una transcripción a nuestro alfabeto— está por ejemplo aquí: http://www.hindilyrix.com/songs/get_song_Mehboob%20mere,%20mehboob%20mere.html).

Frases para el recuerdo

En los tiempos de los apostóles
los hombres eran muy barbáros:
se subían a los arbóles
y se comían los pajáros.

(Tildes añadidas para enfatizar la pronunciación).

Solución al problema de la cebra

Vamos con la solución al puzle de la cebra.

Recordemos las pistas:

1. 1=B5
2. 3=E3
3. A1=D2
4. A2=B1
5. A5=E1
6. B2=E4
7. B3=D1
8. B4=C5
9. C4=D3
10. D4=E5
11. A4|B5
12. C1|D5
13. C3|D2
14. A3|A5
15. A3<A5

Ponemos en un casillero los símbolos, de tal forma que en cada casilla estén todos los símbolos de una fila. Para esto se puede emplear OOCalc, que es lo que he hecho.

	1	2	3	4	5
A	A1A2A3A4A5	A1A2A3A4A5	A1A2A3A4A5	A1A2A3A4A5	A1A2A3A4A5
B	B1B2B3B4B5	B1B2B3B4B5	B1B2B3B4B5	B1B2B3B4B5	B1B2B3B4B5
C	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5
E	E1E2E3E4E5	E1E2E3E4E5	E1E2E3E4E5	E1E2E3E4E5	E1E2E3E4E5

Aplicamos las pistas 1, 2 y 11 para hallar la posición de B5, E3 y A4.

	1	2	3	4	5
A	A1A2A3A4A5	A4	A1A2A3A4A5	A1A2A3A4A5	A1A2A3A4A5
B	B5	B1B2B3B4B5	B1B2B3B4B5	B1B2B3B4B5	B1B2B3B4B5
C	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5
E	E1E2E3E4E5	E1E2E3E4E5	E3	E1E2E3E4E5	E1E2E3E4E5

Cada vez que consigamos averiguar el símbolo de una casilla, lo tachamos (borramos) de todas las demás casillas de esa fila:

	1	2	3	4	5
A	A1A2A3A5	A4	A1A2A3A5	A1A2A3A5	A1A2A3A5
B	B5	B1B2B3B4	B1B2B3B4	B1B2B3B4	B1B2B3B4
C	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5
E	E1E2E4E5	E1E2E4E5	E3	E1E2E4E5	E1E2E4E5

Ahora vamos recorriendo las pistas repetidamente. Para cada igualdad, hemos de comprobar si en las columnas donde aparece cada uno de los dos miembros también está el otro; si no es así, debemos tachar el extra. Por ejemplo, aplicando la pista 3 (A1=D2), puesto que en la 2ª columna no hay A1, hemos de quitar D2 de la misma:

	1	2	3	4	5
A	A1A2A3A5	A4	A1A2A3A5	A1A2A3A5	A1A2A3A5
B	B5	B1B2B3B4	B1B2B3B4	B1B2B3B4	B1B2B3B4
C	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D1D2D3D4D5	D1D3D4D5	D1D2D3D4D5	D1D2D3D4D5	D1D2D3D4D5
E	E1E2E4E5	E1E2E4E5	E3	E1E2E4E5	E1E2E4E5

Repetimos con las pistas 4, 5, 6, 7, 8 y 10:

	1	2	3	4	5
A	A1A3A5	A4	A1A2A3	A1A2A3A5	A1A2A3A5
B	B5	B2B3B4	B1B3B4	B1B2B3B4	B1B2B3B4
C	C1C2C3C4	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D2D3D4D5	D1D3D4D5	D1D2D3D5	D1D2D3D4D5	D1D2D3D4D5
E	E1E2E5	E2E4E5	E3	E1E2E4E5	E1E2E4E5

Al examinar la pista 13, observamos que en la columna 2 no hay D2, por lo tanto en la columna 1 no puede haber C3. Al aplicar la pista 14, podemos tachar A3 y A5 de la columna 1. Como se queda solo A1 en la primera fila, lo tachamos de las demás celdas de esa fila (a partir de ahora lo haremos sin avisar). De acuerdo con la pista 15, A3 no puede estar a la derecha del todo, así que lo tachamos también. Después de todos esos cambios, queda esto:

	1	2	3	4	5
A	A1	A4	A2A3	A2A3A5	A2A5
B	B5	B2B3B4	B1B3B4	B1B2B3B4	B1B2B3B4
C	C1C2C4	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D2D3D4D5	D1D3D4D5	D1D2D3D5	D1D2D3D4D5	D1D2D3D4D5
E	E1E2E5	E2E4E5	E3	E1E2E4E5	E1E2E4E5

Cuando al comprobar una de las igualdades, uno de los miembros está solo, el otro debe estarlo también. Aplicando ese principio a la pista 3 en este punto, hay que dejar solo D2 en la columna 1:

	1	2	3	4	5
A	A1	A4	A2A3	A2A3A5	A2A5
B	B5	B2B3B4	B1B3B4	B1B2B3B4	B1B2B3B4
C	C1C2C4	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D2	D1D3D4D5	D1D3D5	D1D3D4D5	D1D3D4D5
E	E1E2E5	E2E4E5	E3	E1E2E4E5	E1E2E4E5

Aplicamos las pistas 5 y 10, quitando E1 y E5, respectivamente, de la columna 1. Ya sabemos quién bebe E2=agua:

	1	2	3	4	5
A	A1	A4	A2A3	A2A3A5	A2A5
B	B5	B2B3B4	B1B3B4	B1B2B3B4	B1B2B3B4
C	C1C2C4	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5	C1C2C3C4C5
D	D2	D1D3D4D5	D1D3D5	D1D3D4D5	D1D3D4D5
E	E2	E4E5	E3	E1E4E5	E1E4E5

Es B5, el noruego. Aplicamos las pistas 13, 8, 9 y ya no podemos seguir por este método:

	1	2	3	4	5
A	A1	A4	A2A3	A2A3A5	A2A5
B	B5	B2B3	B1B3B4	B1B2B3B4	B1B2B3B4
C	C1C2	C3	C1C2C4C5	C1C2C4C5	C1C2C4C5
D	D2	D1D4D5	D1D3D5	D1D3D4D5	D1D3D4D5
E	E2	E4E5	E3	E1E4E5	E1E4E5

Vamos a hacer un ensayo para falsar una hipótesis. Supongamos que en la columna 2 va E5 y no E4. Entonces, por la pista 10, tiene que ir D4 ahí. Por la pista 7, no puede ir B3 en esa columna, luego tiene que ser B2; pero ahora esto se contradice con la pista 6, que dice que donde va B2 tiene que ir E4. La conclusión es que en la columna 2 no puede ir E5. Lo tachamos y continuamos, aplicando las pistas 6, 10 y 7:

	1	2	3	4	5
A	A1	A4	A2A3	A2A3A5	A2A5
B	B5	B2	B1B3B4	B1B3B4	B1B3B4
C	C1C2	C3	C1C2C4C5	C1C2C4C5	C1C2C4C5
D	D2	D5	D1D3	D1D3D4	D1D3D4
E	E2	E4	E3	E1E5	E1E5

Nuevo punto muerto. Este es más complicado. Vamos a ensayar primero poniendo E1 en la columna 4 y viendo si nos conduce a una contradicción. Aplicamos las pistas 5, 10, 9, 15, 4, 8 y llegamos a este resultado provisional:

	1	2	3	4	5
A	A1	A4	A3	A5	A2
B	B5	B2	B3B4	B3B4	B1
C	C1C2	C3	C1C2C4C5	C1C2C4C5	C1C2
D	D2	D5	D1D3	D1D3	D4
E	E2	E4	E3	E1	E5

Ahora, si ponemos B3 en la columna 3, por la pista 7 tiene que ir D1 en la misma columna, luego en la columna 4 tiene que ir D3, y por la pista 9 va C4 en la misma. Pero esto se contradice con la pista 8, ya que en la columna 4 sólo puede ir B4. Y si ponemos B3 en la columna 4 en vez de la 3, tenemos exactamente el mismo problema. Pongamos donde pongamos B3, llegamos a una contradicción. La única conclusión posible es que E1 no puede ir en la columna 4.

Antes de seguir, una nota. En este punto se puede recurrir a una técnica del Sudoku que consiste en lo siguiente. Las columnas 1 y 5 tienen ambas C1 y C2, aunque no sabemos en qué orden. Esto quiere decir que o la 1 tiene C1 y la 5 C2, o viceversa, no hay otra posibilidad. En cualquiera de los dos casos, podemos tachar C1 y C2 de las columnas 3 y 4. Después de hacerlo, podemos recurrir a la pista 12 para asignar C1 a la columna 1, con lo que en la columna 5 iría C2. Esta es la solución parcial errónea a la que aludía al plantear el problema: C2 está en la columna correcta, como veremos, pero B1 no es la respuesta.

Volvemos al punto muerto anterior, ponemos E5 en la columna 4 y continuamos. Aplicamos las pistas 10, 5, 14, 4, 7, 9, 8, 12 y obtenemos la solución:

	1	2	3	4	5
A	A1	A4	A2	A3	A5
B	B5	B2	B1	B4	B3
C	C1	C3	C4	C5	C2
D	D2	D5	D3	D4	D1
E	E2	E4	E3	E5	E1

O sea, el dueño de C2 (la cebra) es B3 (el japonés).

¿Quién es el dueño de la cebra?

Cuando era niño, vi en una revista un pasatiempo que me resultó muy curioso. Lo copié y lo repartí a mis compañeros y hubo cierto revuelo con el mismo. Se ha divulgado en otras formas, pero aún permanecen en mi memoria las frases del planteamiento y la solución tal y como figuraban en la revista.

Decía así (disculpas por la propaganda de tabacos, que sospecho que estaba detrás de esa publicación, pero he preferido dejar el texto original tal y como lo conocí):

1. Hay cinco casas de distinto color con individuos de diferentes nacionalidades. También hay distintos animales, cigarrillos y bebidas en cada una de ellas.
2. El inglés vive en la casa roja.
3. El español es el propietario del perro.
4. En la casa verde se bebe café.
5. El ucraniano bebe té.
6. La casa verde está contigua y a la derecha (la derecha del lector) de la casa de marfil.
7. El fumador de Winston tiene caracoles.
8. En la casa amarilla se fuma Camel.
9. En la casa del centro se bebe leche.
10. El noruego vive en la primera casa de la izquierda.
11. El hombre que fuma Chesterfield vive en la casa contigua a la del dueño del zorro.
12. En la casa contigua a aquella donde se encuentra el caballo se fuma Camel.
13. El fumador de Lucky Strike bebe naranjada.
14. El japonés fuma Philip Morris.
15. El noruego vive al lado de la casa azul.

Las preguntas eran: ¿quién bebe agua? y ¿quién es el dueño de la cebra?

La respuesta a la primera pregunta es relativamente fácil, pues surge al poco tiempo de ir aplicando pistas. La segunda requiere llegar hasta el final, lo cual requiere bastante más esfuerzo.

Se puede abstraer este problema de la siguiente manera: sea un casillero de 5 filas y 5 columnas, en el que se deben colocar los símbolos A1, A2, A3, A4, A5, B1 a B5, C1 a C5, D1 a D5 y E1 a E5, cada uno en una casilla. Las letras indican la fila en la que colocarlos, pero los dígitos NO indican la columna; en este caso he escogido una permutación al azar de los números del 1 al 5 para cada fila. Para saber en qué columna colocar cada uno, necesitaremos las pistas. Usaremos la siguiente notación:

• n=símbolo indica que en la columna n ha de ir el símbolo dado. Por ejemplo, 1=A4 indica que el símbolo A4 se debe colocar en la fila A, columna 1.
• símbolo1=símbolo2 indica que ambos están en la misma columna.
• símbolo1|símbolo2 indica que están en columnas adyacentes.
• símbolo1<símbolo2 indica que símbolo1 está a la izquierda de símbolo2 (no necesariamente adyacentes).

Las pistas equivalentes para este problema (no en el orden original) son:

1. 1=B5
2. 3=E3
3. A1=D2
4. A2=B1
5. A5=E1
6. B2=E4
7. B3=D1
8. B4=C5
9. C4=D3
10. D4=E5
11. A4|B5
12. C1|D5
13. C3|D2
14. A3|A5
15. A3<A5

Y las preguntas son: ¿qué simbolo hay en la fila B en la misma columna donde está E2? ¿Qué símbolo hay en la fila B en la misma columna donde está C2? Es decir, hallar x e y tales que Bx=E2 y By=C2.

Al principio iba a preguntar en qué columna van E2 y C2, pero después me lo he pensado, dado que hay una solución parcial errónea que tiene C2 en la columna correcta, pero no tiene el símbolo bueno en la fila B de dicha columna. Aquí se busca la solución correcta.

Nótese que las dos últimas pistas juntas equivalen a la Nº. 6 del problema original, pero he querido hacerlo más general por si revisitamos este tipo de acertijos en el futuro.

La equivalencia con el problema anterior es: A1=Amarilla, A2=Roja, A3=Marfil, A4=Azul, A5=Verde; B1=Inglés, B2=Ucraniano, B3=Japonés, B4=Español, B5=Noruego; C1=Zorro, C2=Cebra, C3=Caballo, C4=Caracoles, C5=Perro; D1=Philip Morris, D2=Camel, D3=Winston, D4=Lucky Strike, D5=Chesterfield; E1=Café, E2=Agua, E3=Leche, E4=Té, E5=Naranjada.

No intente hacer esto en su oficina

SignPost es otro nuevo juego en la colección de puzles de Simon Tatham. Partiendo de la casilla 1, hay que avanzar un número indeterminado de casillas en cada paso en la dirección de la flecha, hasta acabar en la que tiene una estrella tras haber recorrido el resto del tablero visitando cada casilla una sola vez. A veces se nos indica en qué paso hay que tocar cierta casilla. Durante la resolución, lo normal es que vayamos conectando partes separadas hasta que tengamos todo conectado.

Como de costumbre, genera problemas con solución única.

No me ha enganchado, pero me ha entretenido, que también es importante.

Paintfuck

Ya hablamos en el artículo Lenguajes esotéricos sobre Brainfuck, un lenguaje de ocho instrucciones sumamente popular. Tanto, que existen multitud de variantes de dicho lenguaje. He aquí unos cuantos:

• En COW se representan la mayoría de instrucciones mediante cambios en las mayúsculas de la palabra «Moo». Es una variante de Brainfuck con cinco instrucciones nuevas.

• FukYorBrane es un lenguaje diseñado para que dos programas en Brainfuck compitan entre sí.

• Brainfork añade una instrucción para convertir el Brainfuck en multitarea.

• Boolfuck y Smallfuck son versiones de Brainfuck que operan sobre bits en vez de palabras.

• Dimensifuck utiliza un casillero n-dimensional en vez de bidimensional.

• Quantum brainfuck opera sobre qubits en vez de sobre enteros. Está basado en la teoría de computación cuántica.

• 2L es una variante bidimensional que usa dos símbolos (y el espacio en blanco).

• Hay muchas más variantes; véase Category: Brainfuck derivatives en la wiki de lenguajes esotéricos.

En particular, el Smallfuck opera sobre un casillero donde cada celda es de un bit. Tiene cinco instrucciones: elimina la entrada y la salida y, como no le hace falta incremento y decremento porque las dos operaciones hacen lo mismo, las sustituye por el comando *, que invierte el bit en la celda actual. Es relativamente sencillo convertir un programa en Brainfuck a Smallfuck (salvo por la entrada/salida), sustituyendo el incremento y decremento por subrutinas que manipulan los bits en bloques de, por ejemplo, 8 bits.

Y del Smallfuck surge el Paintfuck. Es una variante creada por Wouter Visser que utiliza un casillero bidimensional en vez de lineal, lo cual en principio no parece nuevo. Lo que lo hace original es que está pensado para que el casillero sea representado en la pantalla, viendo en tiempo real y de forma animada cómo el programa actúa sobre el mismo.

Las instrucciones < y > son sustituidas por n, s, e, w para los cuatro puntos cardinales respectivos. Las demás instrucciones son idénticas a las de Smallfuck, así que consta de siete instrucciones en total. Todo carácter que no sea una instrucción válida (incluyendo las versiones en mayúsculas de los comandos) se considera un comentario y por tanto no interviene en el programa, pero tampoco causa error. Por ello, es común que los comentarios intercalados se escriban en mayúsculas, para evitar escribir accidentalmente alguna de las letras n, s, e o w que influirían en el comportamiento del programa. El espacio de datos está inicialmente vacío (todo ceros).

Aunque es un lenguaje Turing-completo cuando se aplica a casilleros infinitos en al menos una dimensión, lo cierto es que los casilleros toroidales finitos suelen ser más interesantes. Así, este sencillo programa rellena todo el casillero de unos, aunque no para nunca:

*[e[s]*]

¿Qué hace este programa? Primero, cambia la casilla inicial de 0 a 1. Esto le permite entrar en el bucle. Ya dentro del bucle, se mueve hacia el este y, si da con una casilla que no es cero, se mueve hacia el sur hasta que encuentre la primera que es cero. Si se parte de un casillero vacío, eso debería ocurrir en la línea siguiente, salvo que llegue al punto inicial, en cuyo caso se quedará enganchado indefinidamente en ese bucle. Tanto si va al sur como si no, pone a 1 la casilla actual (era 0 seguro, o de lo contrario no habría salido del bucle anterior) y repite.

Programar en Paintfuck tiene el aliciente de que vemos cómo se desarrolla nuestro programa. Además, trabajar con bits es más simple en general. Entre los programas actualmente escritos en Paintfuck hay, por ejemplo, uno para hacer funcionar el autómata del Juego de la Vida de Conway del que hablamos en la entrada sobre autómatas celulares; también hay otro autómata finito llamado la hormiga de Langton y un contador decimal.

El contador decimal, escrito por un servidor de ustedes, representa cada número dentro de un bloque de 3×5, y se basa en una sugerencia dada en el canal de IRC #esoteric sobre realizar tal contador analizando cada dígito para ver de cuál se trata e incrementarlo. Requirió bastante esfuerzo diseñar la fuente, hallar los píxels distintivos únicos de cada número y analizar los cambios que convertían cada dígito en el siguiente. El programa final es este:

PAINTFUCK PROGRAM BY PEDRO GIMENO 2008-12-01.

swwww*es*ww*s*ee*s*ww*sseeee*wwnw*ww
*[*
  nnee[*ww*s*nee]ww[*ee*ww]s
  *[*ne[*w*n*se]w[*e*w]n
    [*ee*e*s*w*w*s*e*e*s*ww*wnn*n]
    s*[*nnee*s*w*es*s*s*e*ww*wnn]*s]
  n*[*
    nee[*ww*s*nee]ww[*ee*ww]s[*nne*ees*w*w*ess*w*w*n]
    s*[*
      nnnee[*ww*s*nee]ww[*ee*ww]s*[*nee*e*s*s*ss*w*w*wn*nn]
      ss*[*
        seee[*www*n*seee]www[*eee*www]n[*e*ee*s*www*n]
        s*[*
          ee[*ww*n*see]ww[*ee*ww]n*[*nnne*ee*sww*sss*e*en*wwws*n]
          s*[*
            nnne[*w*s*ne]w[*e*w]s*[*nnee*sw*s*ee*ss*w*w*wn*n]
            s*[*
              nnne[*w*s*ne]w[*e*w]s[*ne*sss*s*wnn*n]
              s*[*
                nneee[*www*s*neee]www[*eee*www]s[*ne*ees*ww*s*see*sw*w*wnn*n]
                s*[*
                  se[*w*n*se]w[*e*w]n[*eee*ssww*n*w*n]
                  s*[*
                    ne*e*ws*s*wwwwws*nn]n]]s]s]]n]]n]
  sss*[
    [*e*]*wwwww]n
*]

Bueno, en realidad esa es la versión no comentada. La versión comentada es bastante más larga [1].

Pueden verse este y otros programas en acción gracias al intérprete de Paintfuck en JavaScript, que también puede servir para quien quiera escribir sus propios programas en Paintfuck.

Referencias

[1] http://www.formauri.es/personal/pgimeno/temp/esoteric/paintfuck/decimal-counter.pfk

Dibujando curvas de Bézier cúbicas

He actualizado el tutorial de GIMP sobre la aplicación de efectos de forma radial para incorporarle una animación que cuando publiqué la entrada no había puesto a punto, aunque pensaba que sería una buena adición para explicar cómo actúa el filtro Coord. polares de GIMP. La animación en cuestión es esta:

Está hecha con un programa que escribí en mi lenguaje favorito para hacer pequeñas utilidades cuya velocidad no es crucial, es decir, en PHP. Cuando me puse a pensarlo, me di cuenta de que para hacer la animación que tenía en mente me iban a ser muy útiles las curvas de Bézier cúbicas. Sin embargo, al mirar el listado de funciones de la librería GD, descubrí que no contaba con funciones de dibujado de estas curvas.

Tenía, pues, unas pocas opciones. Una era buscar algún otro módulo PHP capaz de dibujarlas. Resulta que el módulo de ImageMagick lo hacía. Pero usar GD tenía sus ventajas para mí, porque va muy al grano y se puede trabajar con imágenes indexadas (es decir, con paleta), y el ImagickDraw no estaba muy bien documentado. Otra era buscar si alguien más había implementado lo mismo. Encontré unas pocas implementaciones, sí, una de ellas de PEAR que parecía que precisaba mucho aprendizaje para usarla, y otra que resultó tener una calidad muy pobre. La tercera opción era hacerme yo una función para dibujarlas. Finalmente me decanté por esa, aprovechando la ocasión para acometer un reto que tenía pendiente desde hace años. Con algún sistema simple me habría bastado, pero quería resolver el problema de forma definitiva para tener una función que dibujara curvas aplicable a cualquier campo, y que me sirviera de referencia en caso de necesitar reescribirla en otro lenguaje.

Métodos iterativos

Así que estuve investigando los métodos que pude encontrar, para hacerme una idea de por dónde atacar el problema. Sabía de antemano que los métodos recursivos daban mejor resultado que el método iterativo simple.

El método iterativo simple

La forma más sencilla de dibujar curvas de Bézier es utilizar la fórmula directamente, escogiendo un incremento de t adecuado que nos permita recorrer el intervalo [0, 1] de forma uniforme, trazando líneas rectas entre cada punto y el anterior. Además, podemos calcular sólo los coeficientes hasta la mitad usando la igualdad B(P₀, P₁, P₂, P₃, t) = B(P₃, P₂, P₁, P₀, 1 - t). Ya conocía este sistema. El problema principal es que no existe un incremento de t adecuado. Si dibujamos demasiados segmentos, podemos encontrarnos con que la línea se engrosa en algunas zonas de forma muy antiestética. Si no dibujamos suficientes, quedarán a la vista los trazos angulosos de los segmentos rectos con que se dibuja la curva. Lo malo es que en ciertas curvas es fácil que se vean ambos defectos a la vez: trazos angulosos y líneas engrosadas. Así que hay que buscar alternativas.

El método iterativo variable

El problema del método iterativo simple radica en que la distancia entre puntos consecutivos (al aplicar un incremento de t constante) no es uniforme. Este problema se podría salvar recurriendo a la fórmula de la velocidad de la curva, que nos da un indicador de cuán grande será el desplazamiento para un t dado. Para una curva que va de P₀ a P₃ con puntos de control P₁ y P₂, la fórmula es:

V(t) = 3·(1 - t)²·(P₁ - P₀) + 6·t ·(1 - t)·(P₂ - P₁) + 3·t²·(P₃ - P₂)

No he probado este método. A primera vista, parece que tiene el problema de que, si los incrementos no son lo suficientemente pequeños, podrían verse los polígonos de nuevo, así que habría que hacerlos lo bastante pequeños. Hacerlos de un píxel puede presentar problemas cuando los trazos son diagonales. Quizá haciéndolos de 2^½ (1,414213...) píxels, que es la distancia entre dos píxels diagonales, o ligeramente superior para evitar problemas de redondeos, fuera suficiente. Tendría que experimentar. Otra pega es que no veo inmediatamente cómo trasladar velocidad a píxels.

Métodos recursivos

En general, los métodos recursivos se basan en subdividir la curva en múltiples segmentos, utilizando el algoritmo de De Casteljau: Sea B(P₀, P₁, P₂, P₃) una curva de Bézier definida por los puntos P₀, P₁, P₂, P₃. Esta curva se puede dividir de forma exacta en dos segmentos, B₀(P₀, P₀₁, P₀₁₂, P₀₁₂₃) y B₁(P₀₁₂₃, P₁₂₃, P₂₃, P₃). El punto P₀ y el punto P₃ coinciden con los de la curva original, ya que son los extremos del segmento curvo y lógicamente tienen que estar cada uno en una de las curva subdivididas. El punto de subdivisión, P₀₁₂₃, también forma parte de la curva, pues esa es precisamente la ventaja del método de De Casteljau.

P₀₁ es un punto situado en la recta entre P₀ y P₁, a distancia relativa t. Es decir, P₀₁ = (1 - t)·P₀ + t ·P₁. Análogamente obtenemos P₂₃ = (1 - t)·P₂ + t ·P₃. Para obtener los puntos que faltan es preciso calcular un punto extra, P₁₂ = (1 - t)·P₁ + t ·P₂. Ahora, P₀₁₂ = (1 - t)·P₀₁ + t ·P₁₂ y P₁₂₃ = (1 - t)·P₁₂ + t ·P₂₃. Por último, P₀₁₂₃=(1 - t)·P₀₁₂ + t ·P₁₂₃. La figura siguiente ilustra el proceso. Cuando t = ½, nos basta con calcular medias entre los puntos.

Método de subdivisión de una curva de Bézier cúbica en dos, en el punto t=0,3. La curva B(P₀, P₁, P₂, P₃) puede ser dividida en las dos curvas B(P₀, P₀₁, P₀₁₂, P₀₁₂₃) y B(P₀₁₂₃, P₁₂₃, P₂₃, P₃).

Los algoritmos recursivos realizan esta subdivisión, normalmente en el punto t=½, y continúan haciendo lo mismo recursivamente con cada uno de los subsegmentos obtenidos. Difieren en la elección del caso base de la recursión.

Método de la colinealidad

Las subdivisiones recursivas van aproximando cada vez más el segmento dividido a un segmento de recta. Si conseguimos determinar en qué momento es tan parecido a una recta que no es distinguible a simple vista, podremos trazar una recta en su lugar y obtener así una muy buena aproximación.

La curva es más plana cuanto más próximos estén los dos puntos de control a la recta que une los puntos origen y final, así que el cálculo de esa distancia es una buena forma de determinar si son casi colineales. Para evitar una raíz, se puede calcular el cuadrado de la distancia en lugar de la distancia misma. La fórmula del cuadrado de la distancia es:

d(P₁, P₀P₃)² = ((P_x3-P_x0)·(P_y1-P_y0) - (P_y3-P_y0)·(P_x1-P_x0))²/((P_x3-P_x0)² + (P_y3-P_y0)²)

y lo mismo cambiando P₁ por P₂.

Actualización 2011-03-23: Tengo pendiente examinar otra forma de evaluar el «grado de colinealidad», que se me ha ocurrido al releer esta entrada. La idea sería utilizar la ecuación de la recta que pasa por P₀ y P₃, rotándola 90° si el valor absoluto de la pendiente es > 1, para hallar el valor de y que se correspondería con el valor de x del punto a comprobar, hallando entonces la diferencia con la y de dicho punto. Esto podría ser más rápido que el cálculo de la distancia aquí nombrado y probablemente sería igualmente efectivo.

Que sean casi colineales no es condición suficiente para poder aproximar la curva como un segmento de P₀ a P₃. Hay otra condición adicional, y es que tanto P₁ como P₂ estén comprendidos entre P₀ y P₃. Si no se impone esta condición, tanto P₁ como P₂ pueden estar fuera del segmento P₀P₃ y el resultado teórico sería una curva que desde uno de los extremos va temporalmente en dirección contraria al otro extremo, y ese fragmento no sería dibujado. Por ejemplo, si consideramos la curva B((0,0), (-3,0), (10,0), (10,0)), los puntos P₁ y P₂ son colineales con P₀P₃ y, pese a ello, la curva se extiende un poco hacia el lado de abscisas negativas.

En casos como el indicado, la subdivisión podría requerir infinitos pasos para el subsegmento que contiene el pico. Para evitarlo, se puede dar un margen de error: si P₂ y P₃ están ambos dentro de un cuadrado rectángulo de tamaño (|P_x3-P_x0|+ε, |P_y3-P_y0|+&epsilon), se consideran buenos.

Este es el método que escogí finalmente. Los resultados son muy decentes y el algoritmo es aceptablemente rápido. Como parámetros, la distancia al cuadrado que puse para considerar los puntos colineales es 0,125 píxels y el ε que escogí es 0,25 (un cuarto de píxel).

Método de la longitud

La longitud de una curva de Bézier puede ser calculada numéricamente, no hay una fórmula explícita general para la misma. Además de mediante una integral que requiere métodos numéricos clásicos y complicados, hay una forma recursiva de aproximarla que, además, nos da un método para dibujarla.

Sea L₀ la longitud del segmento P₀P₃ y L₁ la suma de las longitudes de los segmentos restantes, concretamente L₁=|P₀P₁| + |P₁P₂| + |P₂P₃|. Entonces, la media de esos valores, (L₁ + L₀) / 2, da una aproximación a la longitud, y L₁ - L₀ da una medida del error. Dicho error decrece en relación 2^-4m donde m es el número de subdivisiones [1].

Se puede entonces dibujar el segmento de forma que si la longitud del subsegmento actual es lo bastante pequeña, se trace dicho subsegmento como recta.

No he probado este método. En realidad es muy similar al anterior, ya que cuando el error es pequeño, significa que los puntos están próximos a ser colineales, lo cual es casi lo mismo que el método anterior. En este no nos salvamos de calcular al menos cuatro raíces cuadradas, por lo cual lo deseché antes de probarlo.

Otros métodos

Descomposición en cuadráticas

En [2] se da una forma de descomponer una curva cúbica en cuatro segmentos de curva cuadrática. No me ha convencido el resultado, pero al menos he creído oportuno dejar una referencia para quien quiera averiguar más. Con este método, queda abierto el problema de cómo dibujar una curva cuadrática de forma eficiente.

Partición de la derivada por octantes

Para terminar, vamos a considerar un método que ha sido utilizado por METAFONT, el programa de diseño tipográfico de D. E. Knuth. Para leer la documentación del programa METAFONT decentemente, necesitaremos la utilidad Weave, capaz de extraer archivos escritos en TeX (el formato de proceso de texto de Knuth) a partir de archivos WEB (que contienen una mezcla del programa en Pascal y la documentación en TeX). El original está aquí: http://mirror.ctan.org/systems/knuth/dist/mf/mf.web. La explicación, junto con el código correspondiente, comienza en la §384.

La idea del método es similar a la de los círculos de Bresenham: se clasifica la derivada de la curva por octantes y se transforma cada uno de los octantes al primero, de manera que la pendiente (el incremento de y por cada incremento unitario de x) no sea superior a la unidad. Con este método se consigue que cada incremento de x vaya asociado a cero o un incremento de y, con lo cual la curva resultante tiene una fineza superior. El precio a pagar por tanto refinamiento es un programa que cuesta mucho entender, además de que cuesta bastantes cálculos. El beneficio es la curva más perfecta posible, igual que la línea de Bresenham es la recta más perfecta posible.

Referencias

[1] http://steve.hollasch.net/cgindex/curves/cbezarclen.html
[2] http://www.timotheegroleau.com/Flash/articles/cubic_bezier_in_flash.htm

Aplicando efectos de forma radial

Hay un filtro para GIMP que puede dar buen resultado aplicado a logos u otros propósitos espectaculares, pero cuya utilidad se ve limitada por la forma en que es aplicado. Estoy hablando de Viento.

El filtro Viento sólo se puede aplicar horizontalmente, hacia la izquierda o hacia la derecha. Esto limita mucho su campo de aplicación, pese a que si pudiera aplicarse de forma radial desde un punto de la imagen hacia los bordes, se podrían conseguir efectos interesantes.

Aquí vamos a ver cómo esquivar esa limitación y aplicar el filtro radialmente. Para ello nos ayudaremos de otro filtro presente en ese mismo menú: Coord. polares.

Hace nada compilé un paquete de Gimp 2.6.8 para Debian Lenny, así que es la versión que vamos a usar en este tutorial. En este caso apenas hay diferencias respecto a la 2.4, pero trataré de explicar las que recuerde.

Primero, dejemos claro el objetivo que perseguimos mediante un par de ejemplos:

Logotipo creado con Archivo > Crear > Logotipos > Calor resplandeciente... (en Gimp 2.4 los logotipos están en el menú Xtns de la ventana de herramientas).

Resultado de aplicar el efecto Viento de forma radial

Peluso

Peluso con efecto viento radial

En el caso del logotipo, para que aparezca el texto bien perfilado he aplicado el efecto solamente a la capa central, ya que la superpuesta ayuda a perfilar; he hecho la prueba de aplanar primero la imagen para aplicar el efecto a todo, pero se emborronaba mucho.

Para ver si el efecto queda aceptable o no, a modo de quickie, bastará con aplicar los pasos cuarto, quinto, sexto, séptimo y noveno (transformación, giro, aplicar efecto, deshacer giro, deshacer transformación), que son los que comprenden la esencia del método. Nos quedará un círculo en pequeño en el centro, pero con suerte bastará para que podamos decidir si vale la pena intentar el método completo o no.

Paso cero: ¿Tiene nuestra capa canal alfa? ¿Lo necesita? ¿Hay que ajustar el color de fondo? ¿Hay que duplicar la capa?

Este tutorial puede aplicarse tanto a capas con canal alfa, como a capas sin él. Al final del proceso, se nos puede haber contaminado la imagen con píxels que no pertenecen a ella, que serán transparentes si hay canal alfa, o del color del fondo si no lo hay. Si tiene alfa, después se puede colocar la imagen original debajo para disimular, pero si se trata de un color plano, basta con asignárselo al color de fondo y nos ahorraremos algún paso. Así que, si no tiene canal alfa, decidamos primero si lo añadimos o no y, en caso de que no, ajustemos el color de fondo. Por ejemplo, si es una capa que contiene un logo en blanco sobre fondo verde homogéneo, se puede ajustar el color de fondo a ese verde y trabajar sin canal alfa. Si lo vamos a hacer con una fotografía, como la de Peluso, lo que mejor resultado proporcione será probablemente duplicar la capa y añadir alfa si no tiene, de manera que la imagen original quede debajo, para que así las partes contaminadas por transparencia dejen a la vista dicha imagen. En cualquier caso, es una buena idea tener una copia de la capa original como referencia, para facilitar el último paso de recorte.

Primer paso: Recentrar

Nuestro primer paso será escoger cuál va a ser el punto central del que van a salir todos los «rayos». En el caso de Peluso, he escogido el punto (284, 276). El filtro Coord. polares toma como centro el de la capa con la que trabaja, así que vamos a ampliar el tamaño de manera que dichos puntos queden en el centro. Si queremos que el centro coincida con el de la imagen, este paso no será necesario. En el caso del logo, he optado por ello y me lo he saltado.

La forma de conseguir el nuevo centro es: averiguar las distancias desde el centro escogido (en coordenadas relativas a la capa) hasta ambos lados de la capa, averiguar la mayor de las dos, y agrandar la capa al doble de dicha distancia, recolocándola de forma que nuestro centro elegido caiga en el centro de la versión agrandada. Esto se hace tanto para la coordenada horizontal como para la vertical. Aquí, «agrandar» no se refiere a escalar, sino a cambiar el tamaño extendiendo el borde. Es la operación que en el Gimp se llama «Tamaño del borde de capa...».

La imagen de Peluso tiene 640×480 píxels. La distancia del centro elegido al borde izquierdo es 284; al borde derecho, es 640-284=356. Por tanto, tenemos que expandir la capa por su lado izquierdo dejando una imagen de 356·2=712 píxels de ancho. Repetimos lo mismo con las coordenadas verticales: la distancia al borde superior es 276 y al borde inferior es 480-276=204 píxels, por lo tanto está más cerca del inferior, luego habrá que expandirlo por debajo hasta que la imagen llegue a 276·2=552 píxels de alto. Es decir, tras redimensionar la capa, ésta ha de quedar pegada a la esquina superior derecha. Así que vamos a Capa > Tamaño del borde de capa, quitamos la cadenita que liga el tamaño vertical y el horizontal e introducimos en Anchura, 712, y en Altura, 552 (píxels, claro). En Desplazamiento, como queremos llevarla a la esquina superior derecha, subimos X al máximo, que es 72, e Y la dejamos a 0. Pulsamos Redimensionar. Ahora el centro de la capa ya es el que queremos.

Segundo paso: Agrandar

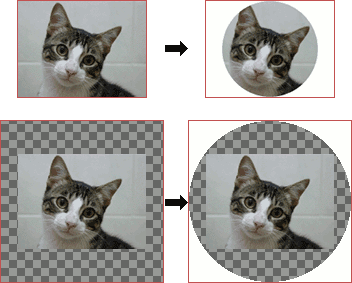
Dada la manera en que vamos a usar el filtro Coord. polares, vamos a tropezar con el problema de que la imagen final va a ser más pequeña que la inicial. Concretamente, con forma de un círculo cuyo diámetro es la menor de las dimensiones de la capa. Para compensar este efecto, hemos de agrandarla de antemano de forma que la parte original quede inscrita dentro de dicho círculo.

Resultado de aplicar el filtro Coord. polares y su inverso. Arriba, sin agrandar la capa primero; abajo, agrandándola. Obsérvese que en la de abajo la imagen original queda completa.

Este tamaño extra se aplica incluso si ya la hemos agrandado en el primer paso, y después de hacerlo; así el botón Centrar hará lo que esperamos.

Para saber el radio del círculo dentro del cual estará nuestra capa inscrita, hemos de echar mano del teorema de Pitágoras. Primero, hay que hallar el centro; esto lo hacemos dividiendo los tamaños horizontal y vertical por 2. Con la imagen de Peluso, el horizontal es 356 y el vertical, 276. El punto más alejado de dicho centro es la esquina (todas ellas), así que hay que calcular la distancia a la misma. Aplicamos Pitágoras: (356²+276²)^½ ~= 450,45. Al final del proceso, debido a errores de precisión acumulados se colarán unos pocos píxels indeseados; para compensarlo, añadimos un 1% (el error máximo que he observado no llega a 0,4% pero más vale estar seguros, ya que va a ser una diferencia pequeña). Redondeamos por lo alto para estar más seguros aún. Buscaremos, pues, un círculo de 455 píxels de radio, o sea, 455·2=910 píxels de diámetro, así que agrandamos la capa para que sea un cuadrado capaz de circunscribir dicho círculo, es decir, le damos un tamaño de 910×910. Para ello, vamos de nuevo a Capa > Tamaño del borde de capa, quitamos la cadenita, introducimos Anchura = 910, Altura = 910 y pulsamos el botón Centrar para que nos centre el contenido actual. Si hemos escogido un centro distinto, podemos ver el resultado un poco descentrado al pulsar el botón; eso es normal y no debe preocuparnos, pero nuestro centro sí debe estar en el centro del cuadrado resultante; si no es así, quizá hemos colocado la capa en el cuadrante incorrecto en el paso anterior y hay que volver atrás. Si todo ha ido bien, pulsamos Redimensionar.

Para el logo, de 526×238, los valores son (263²+119²)^½ ~= 288,67, que multiplicado por 2,02 (el doble más el 1%) y redondeado al alza nos da que la capa debe ser de 584×584.

Tercer paso: Extender los bordes

La capa del logo con la que vamos a trabajar no llega hasta los bordes, así que si se contamina un borde con transparencia a causa de los errores de precisión, no pasa nada; en ese caso podemos pasar al paso siguiente. El caso de Peluso es distinto, porque la fotografía sí que llega hasta los bordes. Si no nos preocupa que se haga un poco transparente en los bordes, podemos saltar este paso. Si estamos aplicando el truco descrito en el Paso Cero, dejando una copia de la imagen en la capa inferior, no lo necesitaremos. Si el borde queda mal incluso al usar esa estratagema, podemos probar con el truco aquí descrito.

La intención es extender cada borde a su correspondiente espacio vacío. No conozco ninguna forma que no sea tediosa. La idea es seleccionar la fila de píxels superior (una selección de Ancho×1), copiarla y pegarla en el espacio vacío superior, escalándola sólo verticalmente y moviéndola para cubrir la totalidad del mismo. Para ver lo que hacemos, es preferible haber hecho primero Imagen > Ajustar lienzo a las capas. Cuando hayamos terminado, hacemos lo mismo con la fila de píxels inferior. Después, con la fila de píxels izquierda (una selección de 1×Alto) y por último, con la derecha. Al hacer la izquierda y la derecha, cogeremos también lo que ya hemos extendido al hacer la parte de arriba y la de abajo.

Por ejemplo, así queda Peluso tras este paso:

Peluso con los bordes extendidos de la forma recién descrita.

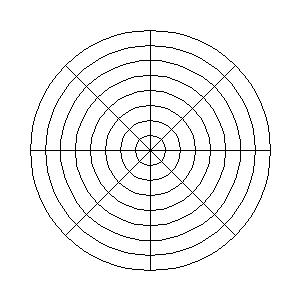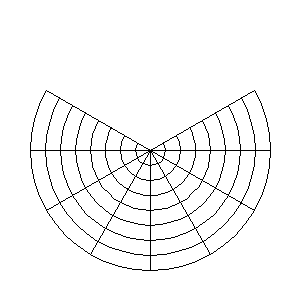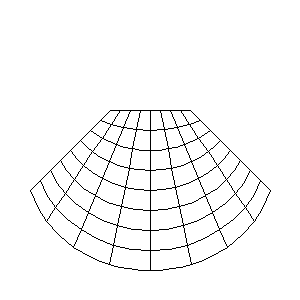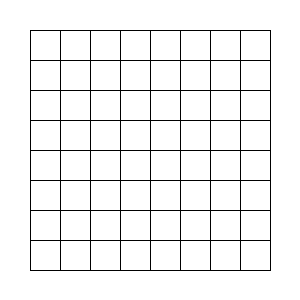
Cuarto paso: Polares a Cartesianas(*)

Vamos al meollo del asunto. Abrimos el filtro Coord. polares y desmarcamos la casilla «A polares», dejando todo lo demás por defecto (profundidad circular 100%, ángulo de desfase 0, no mapear al revés, sí mapear desde arriba). Obtenemos una versión deformada de la imagen de partida. La transformación interpreta la imagen original como si estuviera en coordenadas polares y representa en el eje X, el ángulo, y en el Y, el radio relativo a la menor de las dos dimensiones de la imagen(*). Es decir, todos los efectos que apliquemos verticalmente se harán sobre el radio. Mmmm, eso se parece a lo que queremos.

Actualización 2-2-2010. Esta animación muestra qué transformación realiza el filtro Coord. Polares al aplicarlo a una imagen habiendo marcado las casillas «Mapear al revés» y «Mapear desde arriba» y con la casilla «A polares» desactivada.

Quinto paso: Rotación de 90° a la izquierda

Pero el efecto Viento no opera en dirección vertical, sino únicamente horizontal, así que antes de aplicarlo, primero rotamos la imagen 90° hacia la izquierda con Capa > Transformar > Rotar 90° en sentido antihorario.

Sexto paso: Aplicar el efecto

Ahora es cuando aplicamos el filtro Viento. Hemos de jugar con los ajustes hasta que consigamos lo que buscamos. En el caso de Peluso, he usado Borde Trasero, Umbral 12 y Fuerza 30, dejando Estilo y Dirección intactos. Con el logo, he usado Borde Delantero, Umbral 10 y Fuerza 100.

Séptimo paso: Rotación de 90° a la derecha

Para poder devolver la imagen a su estado inicial con el efecto aplicado, tenemos que deshacer las transformaciones que hemos acumulado. Primero, la giramos a la derecha 90° con Capa > Transformar > Rotar 90° en sentido horario.

Octavo paso: Ampliar (Antialias primera parte)

El filtro Viento produce unas líneas muy finas, de un píxel de ancho, lo cual causa problemas de aliasing al convertir la imagen de nuevo a polares(*), que sería el paso siguiente si no fuera por ese problema. Según la imagen, podemos tener suerte o no, y no he encontrado otra forma de averiguarlo que el ensayo y error. Con Peluso no lo he necesitado; con el logo, sí.

Para conseguir un antialiasing que palie esa pega, el truco que empleamos es ampliar la imagen en este momento, de tal forma que las líneas que se convertirán de cartesianas a polares(*) sean más gruesas, para que después, al reducir con Sinc una vez convertido, sea la propia interpolación la que consiga el antialias. Así que, si hemos tenido en un intento anterior problemas de aliasing, ahora es el momento de ampliar la capa usando Capa > Escalar capa. Recomiendo un valor que no sea un múltiplo exacto como 200%, porque lo he probado y ha sido un fracaso; en cambio, usando un 121% de ampliación he tenido éxito.

Aquí se ve la diferencia sin antialias y con él:

Comparación entre no usar antialias y usarlo

Noveno paso: Cartesianas a Polares(*)

Abrimos de nuevo Coord. polares y marcamos la casilla «A polares» sin tocar nada más. En la previsualización, veremos ya un anticipo del resultado final. Aceptamos.

Actualización 2-2-2010. Esta animación muestra qué transformación realiza el filtro Coord. Polares al aplicarlo a una imagen habiendo marcado las casillas «Mapear al revés» y «Mapear desde arriba» y con la casilla «A polares» activada.

Décimo paso: Reducción (Antialias segunda parte)

Ahora hay que deshacer la ampliación realizada en el octavo paso, si la hemos hecho. Para ello, podemos usar como tamaño destino el tamaño de la imagen en píxels obtenido en el segundo paso (910×910 para Peluso).

Undécimo y último paso: Recortar

Ya solo falta recortar la capa. Esto puede ser complicado si no tenemos una capa de referencia con el tamaño y la posición originales. Si contamos con ella, podemos seleccionarla, usar Capa > Transparencia > Alfa a selección, y luego elegir la capa procesada y usar Capa > Recortar a la selección. Esta última opción no recuerdo que estuviera en Gimp 2.4, así que a quien lo tenga puede que le toque hacer el recorte artesanalmente.

(*): Yo diría que la caja de selección «A polares» está al revés: que cuando está desmarcada es cuando convierte a coordenadas polares y viceversa, representando en un eje el ángulo y en el otro el radio. Por tanto, la primera transformación sería de cartesianas a polares y la transformación inversa convertiría de polares a cartesianas, y no al revés como indica la casilla. Agradecería opiniones al respecto.

Variaciones

El efecto Viento no es el único que se beneficia de esta técnica, así que hay otras opciones para los pasos quinto a séptimo. Otro efecto que no se puede aplicar radialmente es Desplazamiento, aunque en este caso tiene la opción de aplicarlo tanto horizontal como verticalmente, por lo cual si queremos probarlo podemos omitir el paso de la rotación de 90°. No he encontrado aún una utilidad al resultado. Otro posible uso es el Desenfoque gaussiano, ajustando el radio X a cero. Más efectos curiosos: Pixelizar, Mosaico de cristal, Ondular, Borrar las otras filas... Lo que se le ocurra a cada uno.

Nota final

Después de escribir este tutorial, me he dado cuenta de que alguien ya había escrito uno similar: http://www.gimpusers.com/tutorials/rays-of-light-behind-text.html. Sin embargo, he preferido publicarlo porque proporciona valor añadido al explicar cómo recentrar y cómo ampliar la capa en caso de que no sea un logo sino otro tipo de imagen, y explica un método de antialiasing más sofisticado que el que sugiere el autor de ese otro tutorial. El hecho de que ambos tutoriales consten de once pasos es mera coincidencia.

Solución al problema de la probabilidad de cada longitud

(English version available)

En la entrada sobre IMAP se preguntaba por la probabilidad de cada posible longitud de la cadena resultante en el generador de palabas al azar. El bucle tenía esta forma:

  for ($i = 0; $i < 7 + mt_rand(0, 4); $i++) /* añadir un carácter */ ;

La clave está en que el número extraído que sirve como condición de final de bucle puede variar en cada iteración. Es diferente de un bucle similar que fijara el número de antemano, porque entra en juego la intersección de sucesos. Veamos por qué y cómo.

En el momento en que $i alcanza el valor 7, si el valor de mt_rand es 0 entonces el bucle termina; si es cualquier otro valor, continúa. Es evidente que la probabilidad de que la longitud sea 7 es 1/5 = 20%.

Cuando el valor de $i es 8, hace falta que mt_rand devuelva 0 ó 1 para que el bucle termine, lo cual ocurrirá dos de cada cinco veces. Sin embargo, para que la longitud alcance el valor 8 es condición que primero mt_rand haya devuelto un valor entre 1 y 4, lo cual ocurrirá 4 de cada 5 veces. No son sucesos independientes. Por tanto, la probabilidad combinada es 4/5 · 2/5 = 8/25 = 32%.

Para que $i llegue a 9, se tienen que dar a la vez que mt_rand devuelva un valor entre 1 y 4 la primera vez, y un valor entre 2 y 4 la segunda vez. Además, el bucle parará cuando mt_rand esté entre 0 y 2, lo cual ocurrirá 3 de cada 5 veces. Combinando las probabilidades, tenemos P(longitud 9) = 4/5 · 3/5 · 3/5 = 36/125 = 28,8%.

Con el mismo razonamiento, la probabilidad de que llegue a 10 es 4/5 · 3/5 · 2/5 · 4/5 = 96/625 = 15,36%.

La que queda podemos calcularla bien siguiendo el mismo razonamiento, ahora que le hemos cogido carrerilla, o bien restando de 1 todas las anteriores: 4/5 · 3/5 · 2/5 · 1/5 · 5/5 = 24/625 = 3,84% = 100% - 20% - 32% - 28,8% - 15,36%.

Resumiendo:

• P(longitud 7) = 20%
• P(longitud 8) = 32%
• P(longitud 9) = 28,8%
• P(longitud 10) = 15,36%
• P(longitud 11) = 3,84%

O sea, será 8 casi una de cada tres veces, seguido de cerca por 9, luego 7, luego 10, y unas pocas veces llegará a longitud 11. Como siempre he dicho, la probabilidad no es intuitiva.

Este programa ayuda a verificar la corrección de los números:

<?php

  $MAX = 10000000;

  $arr = array(0, 0, 0, 0, 0);

  for ($n = 0; $n < $MAX; $n++)
  {
     for ($i = 0; $i < mt_rand(0, 4); $i++)
       ;
     $arr[$i]++;
  }

  $l = strlen($MAX);
  for ($i = 0; $i < 5; $i++)
  {
    printf("%2d -> %{$l}d/$MAX = %f%%\n", $i+7, $arr[$i], $arr[$i]/$MAX*100);
  }

?>

Aquí el resultado de una ejecución de muestra:

 7 ->  2000626/10000000 = 20.006260%
 8 ->  3198181/10000000 = 31.981810%
 9 ->  2879481/10000000 = 28.794810%
10 ->  1538148/10000000 = 15.381480%
11 ->   383564/10000000 = 3.835640%

Solution to the probability of lengths problem

In the previous IMAP upload post, I asked about the probability of each possible length of the resulting string in the random words generator. The loop had this structure:

  for ($i = 0; $i < 7 + mt_rand(0, 4); $i++) /* add one character */ ;

The key is that the loop exit condition is checked against (probably) different values each time. It's different from a similar loop in which the random number is fixed beforehand, because here the intersection of events comes into play, Let's see why and how.

As soon as $i reaches 7, if the value of mt_rand is 0 then the loop finishes; if it's any other value, it goes on. It's obvious that the probability of the length being 7 is 1/5 = 20%.

When the value of $i is 8, it's necessary for mt_rand to return either 0 or 1 for the loop to end, which will happen one two out of five times. However, for the length to reach the value 8 it's a condition that first mt_rand returns a value between 1 and 4, which will happen 4 out of 5 times. They are not independent events. Therefore, the combined probability is 4/5 · 2/5 = 8/25 = 32%.

For $i to reach 9, it must happen simultaneously that mt_rand returns a value between 1 and 4 the first time, and a value between 2 and 4 the second time. Furthermore, the loop will end when mt_rand is between 0 and 2, which wil happen 3 out of 5 times. Combining the probabilities, we have P(length 9) = 4/5 · 3/5 · 3/5 = 36/125 = 28.8%.

By the same reasoning, the probability for it to reach 10 is 4/5 · 3/5 · 2/5 · 4/5 = 96/625 = 15.36%.

The remaining one can be calculated either following the same reasoning, now that we got the trick, or by subtracting all the previous probabilities from 1: 4/5 · 3/5 · 2/5 · 1/5 · 5/5 = 24/625 = 3.84% = 100% - 20% - 32% - 28.8% - 15.36%.

To sum up:

• P(length 7) = 20%
• P(length 8) = 32%
• P(length 9) = 28.8%
• P(length 10) = 15.36%
• P(length 11) = 3.84%

That is, it will be 8 almost one out of three times, closely followed by 9, then 7, then 10, and a few times it will reach 11. As I have always said, probability is not intuitive.

This program helps verifying the correctness of the numbers:

<?php

  $MAX = 10000000;

  $arr = array(0, 0, 0, 0, 0);

  for ($n = 0; $n < $MAX; $n++)
  {
     for ($i = 0; $i < mt_rand(0, 4); $i++)
       ;
     $arr[$i]++;
  }

  $l = strlen($MAX);
  for ($i = 0; $i < 5; $i++)
  {
    printf("%2d -> %{$l}d/$MAX = %f%%\n", $i+7, $arr[$i], $arr[$i]/$MAX*100);
  }

?>

Sample output:

 7 ->  2000626/10000000 = 20.006260%
 8 ->  3198181/10000000 = 31.981810%
 9 ->  2879481/10000000 = 28.794810%
10 ->  1538148/10000000 = 15.381480%
11 ->   383564/10000000 = 3.835640%

Subida automática de archivos a GMail mediante IMAP

(English version available)

Hace un tiempo había una librería llamada libgmail capaz de comunicarse con GMail usando su protocolo propietario. Sin embargo, los protocolos propietarios tienen un problema muy grave: pueden cambiar en cualquier momento sin previo aviso, y cuando eso ocurre, los que han hecho la ingeniería inversa tienen que averiguar qué cambios se han producido para adaptarlos. Además, hay una norma expresa en los términos de servicio de Google prohibiendo el acceso «por ningún otro medio distinto de la interfaz facilitada por Google». Si se combina eso con el hecho de que libgmail está abandonado desde hace tiempo, puede uno imaginarse el resultado: libgmail ya no se puede utilizar.

Sin embargo, hay otras maneras de usar GMail para subir archivos adjuntos de forma automática. La que probablemente proporcione mayor flexibilidad es usar el protocolo IMAP para realizar las transferencias. El acceso IMAP es proporcionado explícitamente por GMail para que los usuarios no necesiten usar la interfaz web y puedan usar un cliente de email que soporte IMAP para manejar el correo, por lo tanto se puede argumentar que el uso de IMAP es acorde a los términos de servicio. No soy abogado, sin embargo, así que pregunte a uno si quiere una garantía legal.

Por desgracia, no hay actualmente ninguna librería similar a libgmail con soporte IMAP en vez del protocolo propietario de GMail. [Actualización 2011-03-09: Me acabo de enterar de que hay una nueva versión de GMailFS que utiliza el protocolo IMAP. Sin embargo, es un sistema de archivos para Linux, no una utilidad de línea de comandos compatible entre sistemas. No conozco aún una herramienta de línea de comandos que esté disponible para varios sistemas, aparte de la aquí presentada.] He escrito un programa en PHP a modo de prueba de concepto de una herramienta así. Es un ejemplo completo que crea en una cuenta de GMail un mensaje con la etiqueta «ftp» y un archivo adjunto, cuyo tipo MIME es «application/octet-stream». El programa requiere que la extensión IMAP esté instalada en PHP. En Debian Lenny, eso significa instalar el paquete php5-imap.

El acceso IMAP debe estar habilitado en la cuenta destino antes de empezar. La etiqueta 'ftp' debe existir previamente, así que debe ser creada antes de intentar subir ningún archivo. Después de la subida, se puede recuperar el archivo mediante la interfaz web de GMail.

Un inconveniente de este sistema comparado con libgmail es que, puesto que se usa la codificación Base64 para los archivos, el tiempo de subida es cerca de un 33% más. Sería posible en teoría subir archivos usando la codificación Base85, que reduce el tiempo extra a un 25%. Sin embargo, en ese caso la recuperación del archivo requeriría un decodificador Base85 y probablemente no sería posible simplemente hacer clic para descargarlo.

He aquí el código PHP, diseñado para usarse con la versión de línea de comandos. La forma de uso es:
php imap-upload.php <archivo_a_subir>

<?php

/**********************************
 *
 * Configuration section
 *
 */

// User name (full email address)
$usr = 'user@gmail.com';

// Password. Leave unset for being asked (sorry, with echo - yuck!)
unset($pwd);

// IMAP server
$svr = 'imap.gmail.com';

// IMAP port
$prt = 993;

// Folder / Tag (must exist prior to running this)
//$folder = '[Gmail]/Drafts'; // This one would use the actual GMail drafts folder.
                              // NOTE: must be localized, e.g. in spanish the name
                              // is '[Gmail]/Borradores'
$folder = 'ftp';  // Same tag used by gmailftpd.py

// Encoding for the filename string we are passing from the command line
$filename_enc = 'UTF-8';

/*
 *
 * End of configuration section
 *
 ***********************************/


// Encode the subject in MIME quoted-printable format as per RFC 2047
function encode_subject($title, $encoding)
{
  $ret = "=?$encoding?Q?";
  $linelength = 9; // length of "Subject: "

  for ($i = 0; $i < strlen($title); $i++)
  {
    if ($linelength >= 65)
    {
      $ret .= "?=\r\n =?$encoding?Q?";
      $linelength = 1; // length of initial space
    }

    if ($title[$i] >= ' ' and $title[$i] <= '~'
        and $title[$i] != '=' and $title[$i] != '?'
        and $title[$i] != '_')
    {
      if ($title[$i] == ' ')
        $ret .= '_';
      else
        $ret .= $title[$i];
      $linelength++;
    }
    else
    {
      $ret .= '=' . strtoupper(bin2hex($title[$i]));
      $linelength += 3;
    }
  }
  return $ret . '?=';
}

// quoted-string for parameters as per RFC 822
function quoted_string($string)
{
  return '"' . strtr($string, array("\\"=>"\\\\",
                                    "\""=>"\\\"",
                                    "\r"=>"\\\r",
                                    "\n"=>"\\\n")) . '"';
}

// grab 7-11 random lowercase letters
function randword()
{
  $result = '';
  for ($i = 0; $i < 7 + mt_rand(0, 4); $i++)
    $result .= chr(mt_rand(0, 25) + 97);
  return $result;
}

$filepath = $argv[1];

if (! isset($filepath))
  die("No filename specified to upload\n");

$filename = basename($filepath);

if ($prt == 993) $prt = ''; else $prt = ':' . $prt;

if (! isset($pwd))
{
  echo "pwd: ";
  $pwd = substr(fgets(STDIN), 0, -1); // remove extra \n
}

// Open the imap stream
$stream = imap_open("\x7B$svr$prt/ssl}$folder", $usr, $pwd);

// Report all possible errors
print_r(imap_errors());

// Exit on trouble
if ($stream === false) die("\nStopping\n");

$rnd1 = randword();
$rnd2 = randword();
$bndr = "------------" . randword() . randword();

$result = imap_append(
            $stream
            , "\x7B$svr$prt/ssl}$folder"
            , "From: $usr"
              . "\r\nTo: $rnd1@$rnd2.com"
              . "\r\nSubject: " . encode_subject($filename, $filename_enc)
              . "\r\nMIME-Version: 1.0"
              . "\r\nContent-type: multipart/mixed;"
              . "\r\n boundary=\"$bndr\""
              . "\r\n"
              . "\r\nThis is a multi-part message in MIME format."
              . "\r\n--$bndr"
              . "\r\nContent-Type: text/plain; charset=$filename_enc; format=flowed"
              . "\r\nContent-Transfer-Encoding: quoted-printable"
              . "\r\n"
              . "\r\n" . imap_8bit($filename)
              . "\r\n"
              . "\r\n--$bndr"
              . "\r\nContent-Type: application/octet-stream;"
              . "\r\n name=" . quoted_string($filename)
              . "\r\nContent-Transfer-Encoding: base64"
              . "\r\nContent-Disposition: attachment;"
              . "\r\n filename=" . quoted_string($filename)
              . "\r\n"
              . "\r\n" . imap_binary(file_get_contents($filepath))
              . "--$bndr--"
              . "\r\n"
              . "\r\n"
            );

if ($result)
  echo "Succeeded adding file\n";
else
  print_r(imap_errors());

$check = imap_check($stream);
echo "There are now ". $check->Nmsgs . " messages in the $folder folder\n";

print_r(imap_errors());

print_r(imap_alerts());

imap_close($stream);

?>

Y de regalo un pequeño rompecabezas. El generador de letras al azar puede generar entre 7 y 11 caracteres. Suponiendo que el generador genera números enteros uniformemente distribuidos entre 0 y 4 inclusive, ¿cuál es la probabilidad de cada una de las longitudes? Una pista: no es 1/5.

Automated upload to GMail via IMAP

Some time ago, there was a Python library called libgmail which was able to communicate with GMail using their proprietary protocol. However, proprietary protocols have a serious drawback: they can be changed at any time without prior notice, and when that happens, those who have reverse-engineered them have to figure out the changes. Furthermore, there's an explicit rule in Google's ToS forbidding access «by any means other than through the interface that is provided by Google». Combine it with the fact that libgmail has now been abandoned for a while, and you can figure out the result: libgmail is no longer usable.

There are, however, other ways of using GMail to do automated attachment uploads. The one that probably provides the most flexibility is to use the IMAP protocol to do the transfers. IMAP access is explicitly provided by GMail so that users do not need to use the web interface and can use an email client that supports IMAP to handle mail, thus it's arguable that using IMAP is in accordance with the ToS. I am not a lawyer, though, so ask one if you want to be sure.

Unfortunately, there's currently no library similar to libgmail which supports IMAP instead of the proprietary GMail protocol. [Update 2011-03-09: I just learned that there's a new version of GMailFS which uses the IMAP protocol. However, it is a filesystem for Linux, not a cross-platform command line utility. I don't know yet of a command line tool that is compatible across systems, besides the one presented here.] I've written a PHP program as a proof-of-concept of such a tool. It's a complete example that creates a message with the tag 'ftp', having an attached file with MIME type 'application/octet-stream', in a GMail account. The program requires the IMAP extension to be installed in PHP. In Debian Lenny, that means to install the package php5-imap.

IMAP access must be enabled in the target GMail account before starting. The files are tagged with the label 'ftp' which must already exist, so create it before trying to upload. After uploading, you can retrieve the file via the GMail web interface.

A drawback when compared to libgmail is that, as it uses Base64 encoding for files, the upload time is about 33% greater. It would be theoretically possible to upload files using Base85 encoding, which reduces the overhead to 25%. However, in that case the retrieval of the file would need a Base85 decoder and it would probably not be possible to just click on the file to download it.

Here's the PHP code, intended for being used with the PHP command line interface. Usage is:
php imap-upload.php <file_to_upload>

<?php

/**********************************
 *
 * Configuration section
 *
 */

// User name (full email address)
$usr = 'user@gmail.com';

// Password. Leave unset for being asked (sorry, with echo - yuck!)
unset($pwd);

// IMAP server
$svr = 'imap.gmail.com';

// IMAP port
$prt = 993;

// Folder / Tag (must exist prior to running this)
//$folder = '[Gmail]/Drafts'; // This one would use the actual GMail drafts folder.
                              // NOTE: must be localized, e.g. in spanish the name
                              // is '[Gmail]/Borradores'
$folder = 'ftp';  // Same tag used by gmailftpd.py

// Encoding for the filename string we are passing from the command line
$filename_enc = 'UTF-8';

/*
 *
 * End of configuration section
 *
 ***********************************/


// Encode the subject in MIME quoted-printable format as per RFC 2047
function encode_subject($title, $encoding)
{
  $ret = "=?$encoding?Q?";
  $linelength = 9; // length of "Subject: "

  for ($i = 0; $i < strlen($title); $i++)
  {
    if ($linelength >= 65)
    {
      $ret .= "?=\r\n =?$encoding?Q?";
      $linelength = 1; // length of initial space
    }

    if ($title[$i] >= ' ' and $title[$i] <= '~'
        and $title[$i] != '=' and $title[$i] != '?'
        and $title[$i] != '_')
    {
      if ($title[$i] == ' ')
        $ret .= '_';
      else
        $ret .= $title[$i];
      $linelength++;
    }
    else
    {
      $ret .= '=' . strtoupper(bin2hex($title[$i]));
      $linelength += 3;
    }
  }
  return $ret . '?=';
}

// quoted-string for parameters as per RFC 822
function quoted_string($string)
{
  return '"' . strtr($string, array("\\"=>"\\\\",
                                    "\""=>"\\\"",
                                    "\r"=>"\\\r",
                                    "\n"=>"\\\n")) . '"';
}

// grab 7-11 random lowercase letters
function randword()
{
  $result = '';
  for ($i = 0; $i < 7 + mt_rand(0, 4); $i++)
    $result .= chr(mt_rand(0, 25) + 97);
  return $result;
}

$filepath = $argv[1];

if (! isset($filepath))
  die("No filename specified to upload\n");

$filename = basename($filepath);

if ($prt == 993) $prt = ''; else $prt = ':' . $prt;

if (! isset($pwd))
{
  echo "pwd: ";
  $pwd = substr(fgets(STDIN), 0, -1); // remove extra \n
}

// Open the imap stream
$stream = imap_open("\x7B$svr$prt/ssl}$folder", $usr, $pwd);

// Report all possible errors
print_r(imap_errors());

// Exit on trouble
if ($stream === false) die("\nStopping\n");

$rnd1 = randword();
$rnd2 = randword();
$bndr = "------------" . randword() . randword();

$result = imap_append(
            $stream
            , "\x7B$svr$prt/ssl}$folder"
            , "From: $usr"
              . "\r\nTo: $rnd1@$rnd2.com"
              . "\r\nSubject: " . encode_subject($filename, $filename_enc)
              . "\r\nMIME-Version: 1.0"
              . "\r\nContent-type: multipart/mixed;"
              . "\r\n boundary=\"$bndr\""
              . "\r\n"
              . "\r\nThis is a multi-part message in MIME format."
              . "\r\n--$bndr"
              . "\r\nContent-Type: text/plain; charset=$filename_enc; format=flowed"
              . "\r\nContent-Transfer-Encoding: quoted-printable"
              . "\r\n"
              . "\r\n" . imap_8bit($filename)
              . "\r\n"
              . "\r\n--$bndr"
              . "\r\nContent-Type: application/octet-stream;"
              . "\r\n name=" . quoted_string($filename)
              . "\r\nContent-Transfer-Encoding: base64"
              . "\r\nContent-Disposition: attachment;"
              . "\r\n filename=" . quoted_string($filename)
              . "\r\n"
              . "\r\n" . imap_binary(file_get_contents($filepath))
              . "--$bndr--"
              . "\r\n"
              . "\r\n"
            );

if ($result)
  echo "Succeeded adding file\n";
else
  print_r(imap_errors());

$check = imap_check($stream);
echo "There are now ". $check->Nmsgs . " messages in the $folder folder\n";

print_r(imap_errors());

print_r(imap_alerts());

imap_close($stream);

?>

Here's a little bonus brainteaser. The generator of random lowercase letters can generate 7 to 11 characters. What's the probability of each length? Hint: it's not 1/5.

Génera y sexa

¿A ustedes no les asombra
que diciendo rico y rica,
majo y maja, chico y chica,
no digamos hombre y hombra?
Y la frase tan oída
del marido y la mujer,
¿por qué no tiene que ser
el marido y la marida?
[...]
El sexo a hablar nos obliga
a cada cual como digo:
si es hombre, me voy contigo;
si es mujer, me voy contiga.
—Melitón González (Pablo Perellada), El idioma castellano (fragmento)

Ya hace mucho que, en el esfuerzo por compensar el machismo tradicional en nuestra sociedad, ciertos grupos están intentando imponer el hembrismo como doctrina. Y no digo feminismo, porque feminismo es otra cosa. El objetivo parece ser la venganza a través del cambio de papeles, así que se trata de sustituir una dominación por la contraria.

En ese empeño de sobrecompensarla hasta el punto de llevarla al polo opuesto, uno de los más equivocados objetivos es la hembrización del lenguaje. Típicamente, se confunde género con sexo y las palabras de género masculino se fuerzan de forma artificial a una versión femenina inexistente. No digo que ello esté siempre mal; la lengua se rige por la tradición y la inexistencia de ciertas palabras puede deberse a la falta de uso previo, por lo que si surge la necesidad, es lógico que aparezcan.

Veamos unos ejemplos. El que maneja una bomba hidráulica para apagar incendios es un bombero; por tanto, si es ella, es bombera. Sí, puede sonarnos extraño, pero dudo que sea por otra razón que la falta de costumbre, pues es el mismo caso que con cajero y cajera, por decir uno. Otro ejemplo más sencillo: el que aboga es abogado y la que aboga, abogada. Aquí, además, contamos con un verbo cuyo participio ya pertenece a nuestro idioma, de modo que la palabra ya existía; por ejemplo, «la reforma abogada por los grupos...» vendría a significar «la reforma por la que los grupos abogan...». No es preciso agregar un vocablo inexistente para referirse a las que ejercen la abogacía.

El problema del hembrismo está en que arrambla con todo tipo de palabras, pese a los absurdos a los que conduce tal política (como con miembra*). Hasta tal punto llega el empeño, que también se han convertido al femenino palabras neutras. ¿Qué me dicen de jueza? Juez es una palabra de género común que no tiene siquiera una terminación clásicamente asociada al género masculino. ¿De quién fue la feliza* idea de apalear así a nuestro idioma? No me lo digan: de las hembristas.

Otro tanto ocurre con presidenta. Si el o la que preside es presidente, ¿a qué tanto empeño en amplificar las diferencias entre sexos, si lo que persigue el feminismo es la igualdad? ¿Está acaso calienta* la que tiene calores? Lo mismo con capitana, edila, concejala, tenienta, bedela... ¿Qué será lo próximo? ¿Caba*, alféreza*, albañila*? ¿Por qué no otros adjetivos menos agradables? ¿Qué tal incordianta*, atroza*, inútila*, gilipóllasa* o, ya puestos, gilicoños*?

No digo que al revés no haya ocurrido; así, hay casos como modisto, que viene de moda, siendo que ya contamos con la palabra neutra modista, que describe lo mismo. Pocos, muy pocos ejemplos similares se podrán encontrar. Puedo comprenderlo (aunque no compartirlo), pues la profesión de modista ha sido siempre asociada a la mujer y la palabra debió de surgir de que alguien, no necesariamente siquiera un varón (quizá incluso la esposa del interfecto), quería recalcar para evitar confusiones que el modista era de sexo masculino, muy machote él. Déjenme recalcar esto: me parece tan aberrante jueza o presidenta como modisto y tan correcto abogada o bombera como prostituto (y hablo únicamente de la corrección del lenguaje, no de las condiciones laborales).

En general, en cambio, al varón no le importa lo más mínimo que sea adjetivado con una palabra acabada en -a: no hay transportistos* ni ordenanzos* ni guíos* ni falta que hace, porque ni la terminación ni el género determinan el sexo. Nadie presiona por que se use idioto* en vez de idiota para los varones. Son, por tanto, las ganas de marcar las diferencias entre sexos por parte de las talibanas de la lengua las que nos llevan a aberraciones como estas. Es hora de detener esta sinrazón.

Estreno de foro en 11-s.eu.org

En nuestra página web del 11-S no teníamos sección de comentarios. Con este propósito estábamos parasitando el foro de Psicopanadero, porque el soft de wiki usado para la web no soporta comentarios. Es un soft a medida que yo desarrollé usando la idea del Giki pero escribiendo el código desde cero. Sin embargo, la adición de una sección de comentarios con todo lo que ello conlleva parecía demasiado trabajo.

Ahora hemos abierto un foro para discutir sobre el 11-S; dentro de él, uno de los subforos hace de sección de comentarios para que se puedan discutir los artículos individualmente, con lo que queda por fin paliada esa falta.

Y más puzles

La colección de Simon Tatham está echando humo. Ahora son tres nuevos juegos más: Towers, Singles y Magnets.

Towers es un poco raro. Se trata de determinar la altura de unas torres (que son números enteros dispuestos en forma de cuadrado latino, de nuevo), una torre por casilla. Las pistas con las que contamos son unos enteros dispuestos alrededor del cuadrado, que indican el número de torres visibles horizontalmente desde el lado en el que se encuentra la pista en cuestión. Las torres más altas ocultan a las más bajas. Por ejemplo, en un casillero de 5×5, si en el lado izquierdo una de las filas tiene un 5 como pista, eso quiere decir que esa fila están los números del 1 al 5 en escala ascendente. Si pone un 3, hay muchas posibilidades y tendremos que valernos de más información para averiguarlo. Si pone un 1, entonces esa fila empieza por un 5, porque es el único que oculta a todos los demás. No me ha parecido interesante; me parece muy artificioso y poco intuitivo. Aunque eso mismo pensaba de Tents y al final sí que le vi la gracia.

Singles es algo más normal. Se nos muestra un cuadrado de n×n (no latino, esta vez) relleno con enteros de 1 a n, algunos repetidos en ciertas filas y columnas. Se trata de tachar todos los repetidos menos uno y dejar únicamente los no repetidos. Como condiciones adicionales, los números tachados no pueden estar adyacentes (arriba/abajo/izquierda/derecha, pero pueden estar en diagonal) y no puede haber grupos aislados de números sin tachar, es decir, se debe poder ir de cualquier número sin tachar a cualquier otro número mediante repetidos movimientos de una casilla cada uno hacia arriba, abajo, a la izquierda o a la derecha, o lo que es también lo mismo, los números no tachados tienen que formar un área conexa. Tiene su encanto.

Por último, en Magnets nos dan un tablero no necesariamente cuadrado, en el que se han dispuesto de antemano una serie de fichas rectangulares de 2×1. Cada una puede ser bien un imán, bien una ficha neutra. Se trata de colocar todos los imanes con su polaridad, respetando dos reglas básicas: una, que el número de signos positivos y el número de signos negativos de una fila o columna coincidan con las pistas que se nos dan (sin embargo, en algunas variantes no se nos dan todas: los que no tienen número no son cero, sino desconocidos), y otra, que no puede haber dos signos + juntos ni dos signos - juntos. Este es el más entretenido de los tres, a mi gusto.

Están todos disponibles para descarga para varias plataformas (Linux, OS X, Android, Windows, Palm) en el sitio de costumbre: http://www.chiark.greenend.org.uk/~sgtatham/puzzles/.