He actualizado el tutorial de GIMP sobre la aplicación de efectos de forma radial para incorporarle una animación que cuando publiqué la entrada no había puesto a punto, aunque pensaba que sería una buena adición para explicar cómo actúa el filtro Coord. polares de GIMP. La animación en cuestión es esta:
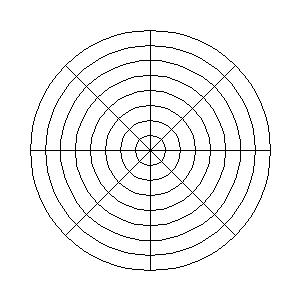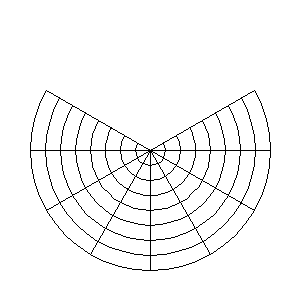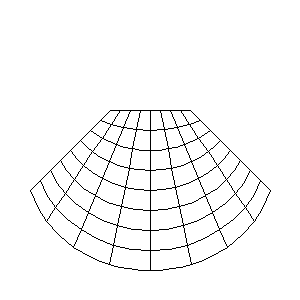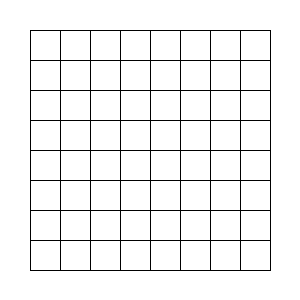
Está hecha con un programa que escribí en mi lenguaje favorito para hacer pequeñas utilidades cuya velocidad no es crucial, es decir, en PHP. Cuando me puse a pensarlo, me di cuenta de que para hacer la animación que tenía en mente me iban a ser muy útiles las curvas de Bézier cúbicas. Sin embargo, al mirar el listado de funciones de la librería GD, descubrí que no contaba con funciones de dibujado de estas curvas.
Tenía, pues, unas pocas opciones. Una era buscar algún otro módulo PHP capaz de dibujarlas. Resulta que el módulo de ImageMagick lo hacía. Pero usar GD tenía sus ventajas para mí, porque va muy al grano y se puede trabajar con imágenes indexadas (es decir, con paleta), y el ImagickDraw no estaba muy bien documentado. Otra era buscar si alguien más había implementado lo mismo. Encontré unas pocas implementaciones, sí, una de ellas de PEAR que parecía que precisaba mucho aprendizaje para usarla, y otra que resultó tener una calidad muy pobre. La tercera opción era hacerme yo una función para dibujarlas. Finalmente me decanté por esa, aprovechando la ocasión para acometer un reto que tenía pendiente desde hace años. Con algún sistema simple me habría bastado, pero quería resolver el problema de forma definitiva para tener una función que dibujara curvas aplicable a cualquier campo, y que me sirviera de referencia en caso de necesitar reescribirla en otro lenguaje.
Métodos iterativos
Así que estuve investigando los métodos que pude encontrar, para hacerme una idea de por dónde atacar el problema. Sabía de antemano que los métodos recursivos daban mejor resultado que el método iterativo simple.
El método iterativo simple
La forma más sencilla de dibujar curvas de Bézier es utilizar la fórmula directamente, escogiendo un incremento de t adecuado que nos permita recorrer el intervalo [0, 1] de forma uniforme, trazando líneas rectas entre cada punto y el anterior. Además, podemos calcular sólo los coeficientes hasta la mitad usando la igualdad B(P0, P1, P2, P3, t) = B(P3, P2, P1, P0, 1 - t). Ya conocía este sistema. El problema principal es que no existe un incremento de t adecuado. Si dibujamos demasiados segmentos, podemos encontrarnos con que la línea se engrosa en algunas zonas de forma muy antiestética. Si no dibujamos suficientes, quedarán a la vista los trazos angulosos de los segmentos rectos con que se dibuja la curva. Lo malo es que en ciertas curvas es fácil que se vean ambos defectos a la vez: trazos angulosos y líneas engrosadas. Así que hay que buscar alternativas.
El método iterativo variable
El problema del método iterativo simple radica en que la distancia entre puntos consecutivos (al aplicar un incremento de t constante) no es uniforme. Este problema se podría salvar recurriendo a la fórmula de la velocidad de la curva, que nos da un indicador de cuán grande será el desplazamiento para un t dado. Para una curva que va de P0 a P3 con puntos de control P1 y P2, la fórmula es:
No he probado este método. A primera vista, parece que tiene el problema de que, si los incrementos no son lo suficientemente pequeños, podrían verse los polígonos de nuevo, así que habría que hacerlos lo bastante pequeños. Hacerlos de un píxel puede presentar problemas cuando los trazos son diagonales. Quizá haciéndolos de 2½ (1,414213...) píxels, que es la distancia entre dos píxels diagonales, o ligeramente superior para evitar problemas de redondeos, fuera suficiente. Tendría que experimentar. Otra pega es que no veo inmediatamente cómo trasladar velocidad a píxels.
Métodos recursivos
En general, los métodos recursivos se basan en subdividir la curva en múltiples segmentos, utilizando el algoritmo de De Casteljau: Sea B(P0, P1, P2, P3) una curva de Bézier definida por los puntos P0, P1, P2, P3. Esta curva se puede dividir de forma exacta en dos segmentos, B0(P0, P01, P012, P0123) y B1(P0123, P123, P23, P3). El punto P0 y el punto P3 coinciden con los de la curva original, ya que son los extremos del segmento curvo y lógicamente tienen que estar cada uno en una de las curva subdivididas. El punto de subdivisión, P0123, también forma parte de la curva, pues esa es precisamente la ventaja del método de De Casteljau.
P01 es un punto situado en la recta entre P0 y P1, a distancia relativa t. Es decir, P01 = (1 - t)·P0 + t ·P1. Análogamente obtenemos P23 = (1 - t)·P2 + t ·P3. Para obtener los puntos que faltan es preciso calcular un punto extra, P12 = (1 - t)·P1 + t ·P2. Ahora, P012 = (1 - t)·P01 + t ·P12 y P123 = (1 - t)·P12 + t ·P23. Por último, P0123=(1 - t)·P012 + t ·P123. La figura siguiente ilustra el proceso. Cuando t = ½, nos basta con calcular medias entre los puntos.
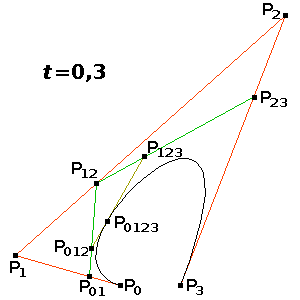
Los algoritmos recursivos realizan esta subdivisión, normalmente en el punto t=½, y continúan haciendo lo mismo recursivamente con cada uno de los subsegmentos obtenidos. Difieren en la elección del caso base de la recursión.
Método de la colinealidad
Las subdivisiones recursivas van aproximando cada vez más el segmento dividido a un segmento de recta. Si conseguimos determinar en qué momento es tan parecido a una recta que no es distinguible a simple vista, podremos trazar una recta en su lugar y obtener así una muy buena aproximación.
La curva es más plana cuanto más próximos estén los dos puntos de control a la recta que une los puntos origen y final, así que el cálculo de esa distancia es una buena forma de determinar si son casi colineales. Para evitar una raíz, se puede calcular el cuadrado de la distancia en lugar de la distancia misma. La fórmula del cuadrado de la distancia es:
y lo mismo cambiando P1 por P2.
Actualización 2011-03-23: Tengo pendiente examinar otra forma de evaluar el «grado de colinealidad», que se me ha ocurrido al releer esta entrada. La idea sería utilizar la ecuación de la recta que pasa por P0 y P3, rotándola 90° si el valor absoluto de la pendiente es > 1, para hallar el valor de y que se correspondería con el valor de x del punto a comprobar, hallando entonces la diferencia con la y de dicho punto. Esto podría ser más rápido que el cálculo de la distancia aquí nombrado y probablemente sería igualmente efectivo.
Que sean casi colineales no es condición suficiente para poder aproximar la curva como un segmento de P0 a P3. Hay otra condición adicional, y es que tanto P1 como P2 estén comprendidos entre P0 y P3. Si no se impone esta condición, tanto P1 como P2 pueden estar fuera del segmento P0P3 y el resultado teórico sería una curva que desde uno de los extremos va temporalmente en dirección contraria al otro extremo, y ese fragmento no sería dibujado. Por ejemplo, si consideramos la curva B((0,0), (-3,0), (10,0), (10,0)), los puntos P1 y P2 son colineales con P0P3 y, pese a ello, la curva se extiende un poco hacia el lado de abscisas negativas.
En casos como el indicado, la subdivisión podría requerir infinitos pasos para el subsegmento que contiene el pico. Para evitarlo, se puede dar un margen de error: si P2 y P3 están ambos dentro de un cuadrado rectángulo de tamaño (|Px3-Px0|+ε, |Py3-Py0|+&epsilon), se consideran buenos.
Este es el método que escogí finalmente. Los resultados son muy decentes y el algoritmo es aceptablemente rápido. Como parámetros, la distancia al cuadrado que puse para considerar los puntos colineales es 0,125 píxels y el ε que escogí es 0,25 (un cuarto de píxel).
Método de la longitud
La longitud de una curva de Bézier puede ser calculada numéricamente, no hay una fórmula explícita general para la misma. Además de mediante una integral que requiere métodos numéricos clásicos y complicados, hay una forma recursiva de aproximarla que, además, nos da un método para dibujarla.
Sea L0 la longitud del segmento P0P3 y L1 la suma de las longitudes de los segmentos restantes, concretamente L1=|P0P1| + |P1P2| + |P2P3|. Entonces, la media de esos valores, (L1 + L0) / 2, da una aproximación a la longitud, y L1 - L0 da una medida del error. Dicho error decrece en relación 2-4m donde m es el número de subdivisiones [1].
Se puede entonces dibujar el segmento de forma que si la longitud del subsegmento actual es lo bastante pequeña, se trace dicho subsegmento como recta.
No he probado este método. En realidad es muy similar al anterior, ya que cuando el error es pequeño, significa que los puntos están próximos a ser colineales, lo cual es casi lo mismo que el método anterior. En este no nos salvamos de calcular al menos cuatro raíces cuadradas, por lo cual lo deseché antes de probarlo.
Otros métodos
Descomposición en cuadráticas
En [2] se da una forma de descomponer una curva cúbica en cuatro segmentos de curva cuadrática. No me ha convencido el resultado, pero al menos he creído oportuno dejar una referencia para quien quiera averiguar más. Con este método, queda abierto el problema de cómo dibujar una curva cuadrática de forma eficiente.
Partición de la derivada por octantes
Para terminar, vamos a considerar un método que ha sido utilizado por METAFONT, el programa de diseño tipográfico de D. E. Knuth. Para leer la documentación del programa METAFONT decentemente, necesitaremos la utilidad Weave, capaz de extraer archivos escritos en TeX (el formato de proceso de texto de Knuth) a partir de archivos WEB (que contienen una mezcla del programa en Pascal y la documentación en TeX). El original está aquí: http://mirror.ctan.org/systems/knuth/dist/mf/mf.web. La explicación, junto con el código correspondiente, comienza en la §384.
La idea del método es similar a la de los círculos de Bresenham: se clasifica la derivada de la curva por octantes y se transforma cada uno de los octantes al primero, de manera que la pendiente (el incremento de y por cada incremento unitario de x) no sea superior a la unidad. Con este método se consigue que cada incremento de x vaya asociado a cero o un incremento de y, con lo cual la curva resultante tiene una fineza superior. El precio a pagar por tanto refinamiento es un programa que cuesta mucho entender, además de que cuesta bastantes cálculos. El beneficio es la curva más perfecta posible, igual que la línea de Bresenham es la recta más perfecta posible.
Referencias
[1] http://steve.hollasch.net/cgindex/curves/cbezarclen.html
[2] http://www.timotheegroleau.com/Flash/articles/cubic_bezier_in_flash.htm

No comments:
Post a Comment